1.0 Summary
We show that by implementing column-major scheduling to improve data locality, we can accelerate the core Triton GEMM (General Matrix-Matrix Multiply) kernel for MoEs (Mixture of Experts) up to 4x on A100, and up to 4.4x on H100 Nvidia GPUs. This post demonstrates several different work decomposition and scheduling algorithms for MoE GEMMs and shows, at the hardware level, why column-major scheduling produces the highest speedup.
Repo and code available at: https://github.com/pytorch-labs/applied-ai/tree/main/triton/.
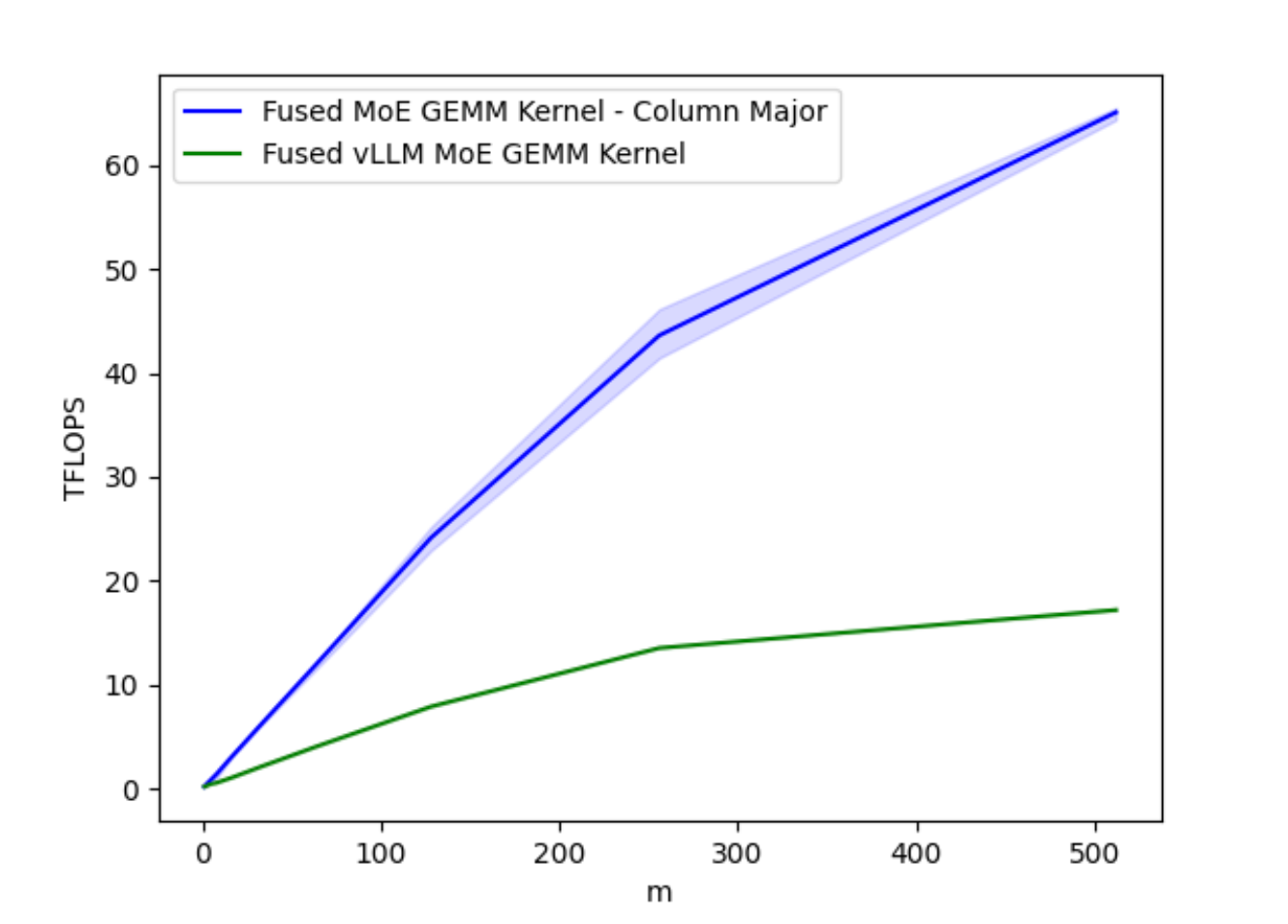
Figure 1A. Optimized Fused MoE GEMM Kernel TFLOPs on A100 for varying Batch Sizes M
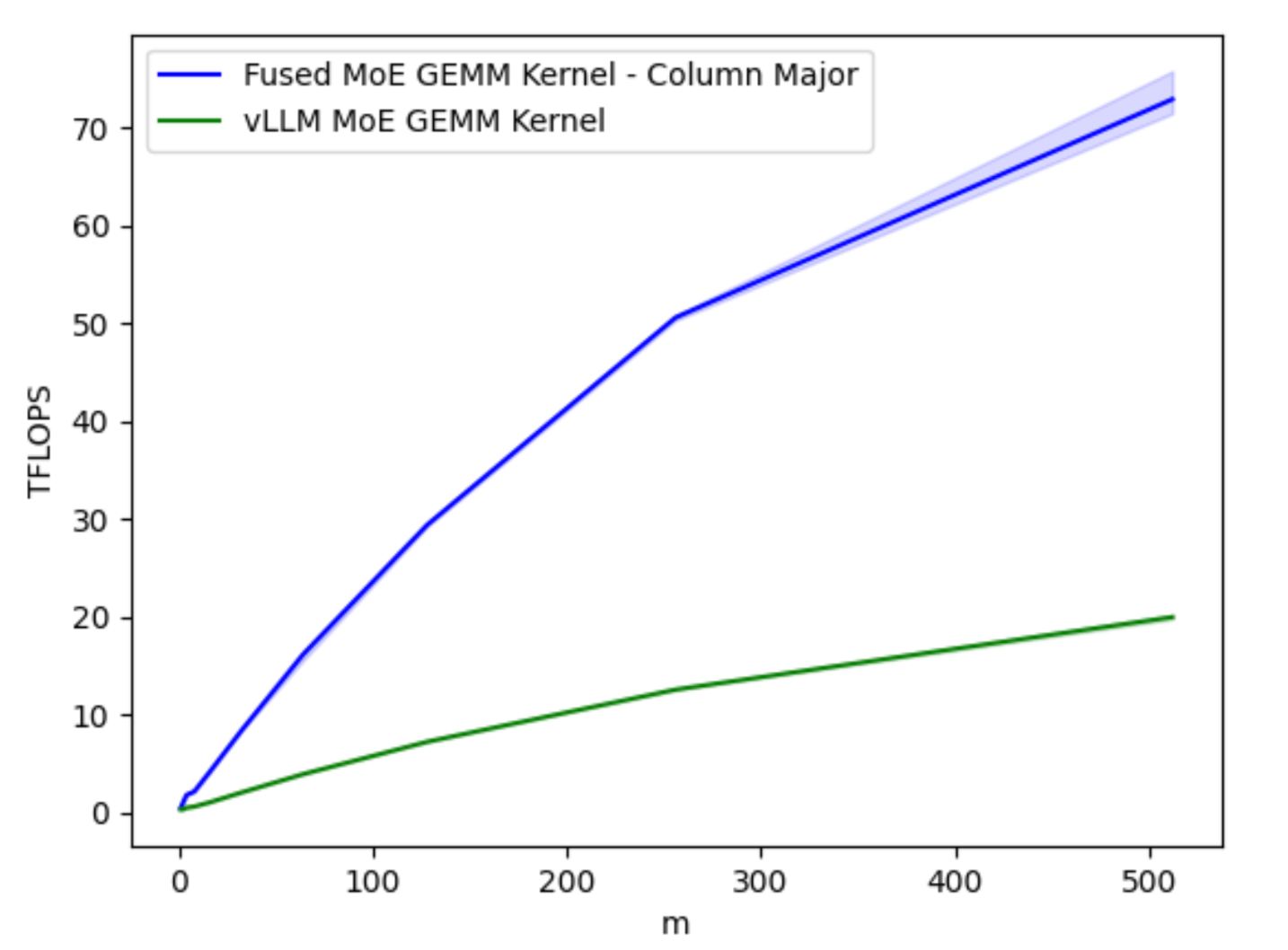
Figure 1B. Optimized Fused MoE GEMM Kernel TFLOPs on H100 for varying Batch Sizes M
2.0 Background
OpenAI’s Triton is a hardware-agnostic language and compiler that as our prior blog post has shown can be used to accelerate quantization workflows. We also showed that in terms of kernel development, much of the same learnings and performance analysis tools from CUDA can be leveraged to provide similar insights into how Triton kernels work under-the-hood and subsequent measures to speedup these kernels in latency sensitive environments. As Triton becomes increasingly adopted in production settings, it is important that developers understand the common tips and tricks to developing performant kernels as well as the generality of these methods to various different architectures and workflows. Thus, this post will explore how we optimized the Triton kernel developed by vLLM for the popular Mixture of Experts (MoE) Mixtral model using classical techniques and how these techniques can be implemented in Triton to achieve performance gain.
Mixtral 8x7B is a sparse Mixture of Experts Language Model. Unlike the classical dense transformer architecture, each transformer block houses 8 MLP layers where each MLP is an ‘expert’. As a token flows through, a router network selects which 2 of the 8 experts should process that token and the results are then combined. The selected experts for the same token vary at each layer. As a result, while Mixtral 8x7B has a total of 47B params, during inference only 13B params are active.
The MoE GEMM (General Matrix-Matrix Multiply) kernel receives a stacked weight matrix containing all the experts, and must subsequently route each token to the TopK (2 for Mixtral) experts by utilizing a mapping array produced by the resultant scores of the router network. In this post, we provide methods to efficiently parallelize this computation during inference time, specifically during autoregression (or decoding stages).
3.0 Work Decomposition – SplitK
We have previously shown that for the matrix problem sizes found in LLM inference, specifically in the context of W4A16 quantized inference, GEMM kernels can be accelerated by applying a SplitK work decomposition. Thus, we started our MoE acceleration research by implementing SplitK in the vLLM MoE Kernel, which produced speedups of approximately 18-20% over the Data Parallel approach.
This result shows that the SplitK optimization can be used as a part of a more formulaic approach to improving/developing Triton kernels in inference settings. To build intuition about these different work decompositions, let’s consider a simple example for the multiplication of two 4×4 matrices and SplitK=2.
In the data parallel GEMM kernel shown below, the computation for a single block of the output matrix will be handled by 1 threadblock, TB0.
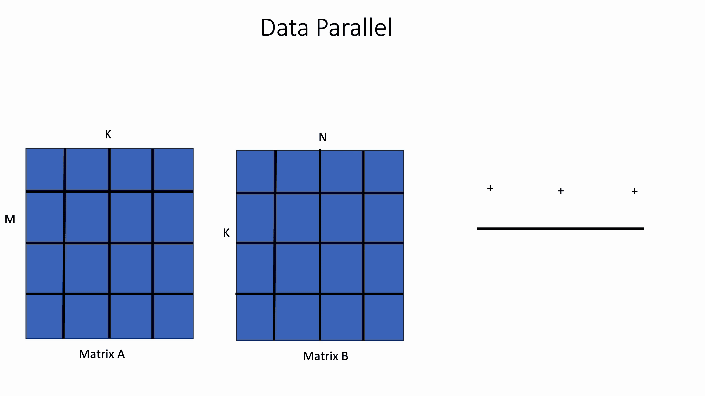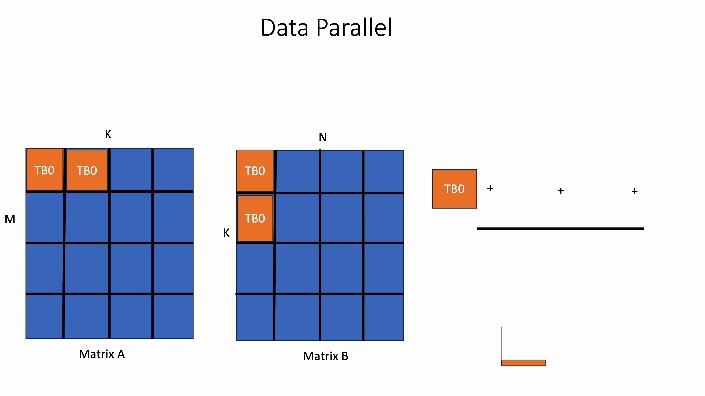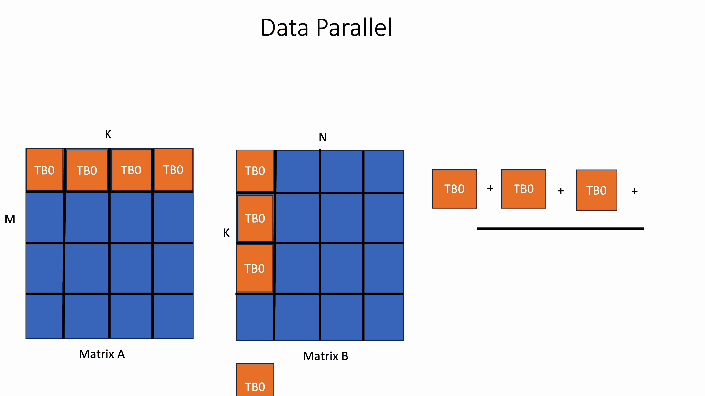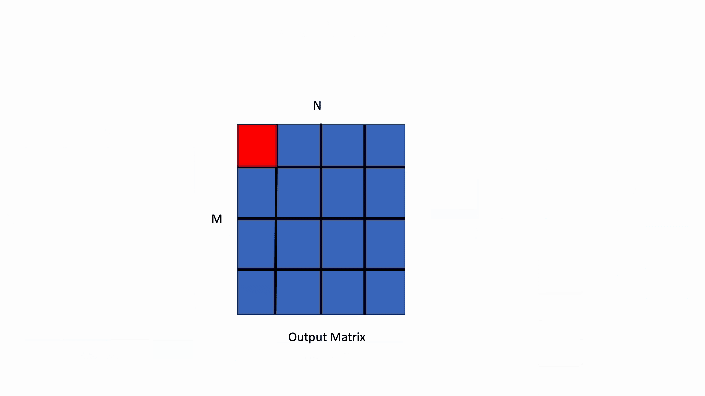
Figure 2. Data Parallel GEMM
In contrast, in the SplitK kernel, the work required to compute 1 block in the output matrix, is “split” or shared amongst 2 thread blocks TB0 and TB1. This provides better load balancing and increased parallelism.
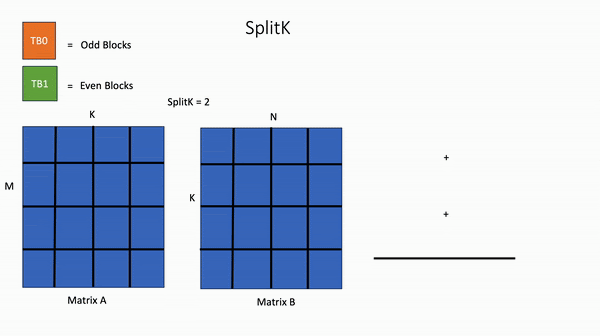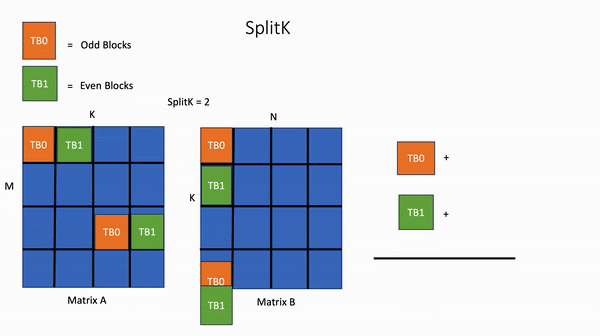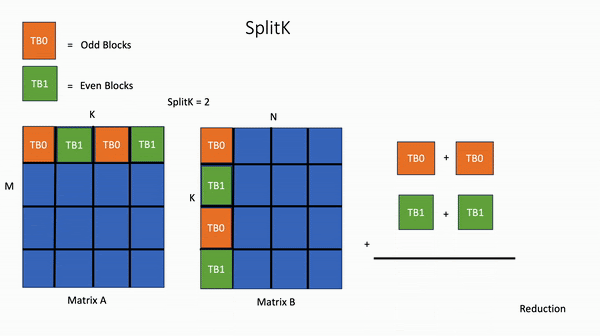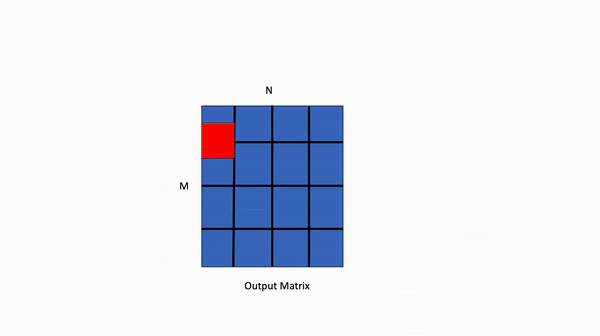
Figure 3. SplitK GEMM
The key idea is that we’ve increased our parallelism from MN to MN*SplitK. This approach does incur some costs such as adding inter-threadblock communication via atomic operations. However, these costs are minimal compared to the savings of other constrained GPU resources like shared memory and registers. Most importantly, the SplitK strategy provides superior load balancing characteristics for skinny matrices, (as is the case in MoE inference) and is the common matrix profile during decoding and inference.
4.0 GEMM Hardware Scheduling – Column Major
To improve upon the ~20% speedup with SplitK we focused our investigation on the logic that controls the hardware scheduling of the GEMM in Triton Kernels. Our profiling of the vLLM MoE kernel showed a low L2 cache hit rate, thus we investigated three scheduling options – column-major, row-major and grouped launch. Due to some intrinsic properties of MoE models, such as large expert matrices, and having to dynamically load TopK (2 for Mixtral) matrices during the duration of the kernel, cache reuse/hit rate becomes a bottleneck that this optimization will target.
For background, in our previous blog, we touched on the concept of “tile swizzling”, a method to achieve greater L2 cache hit rate. This concept relates to how the software schedules the GEMM onto the SMs of a GPU. In Triton, this schedule is determined by the pid_m and pid_n calculations. Our key insight is that for skinny matrix multiplications, a column-major ordering ensures optimal reuse of the columns of the weight matrix, B. To illustrate this, let’s take a look at a snippet of what a column major computation of pid_m, and pid_n would look like:
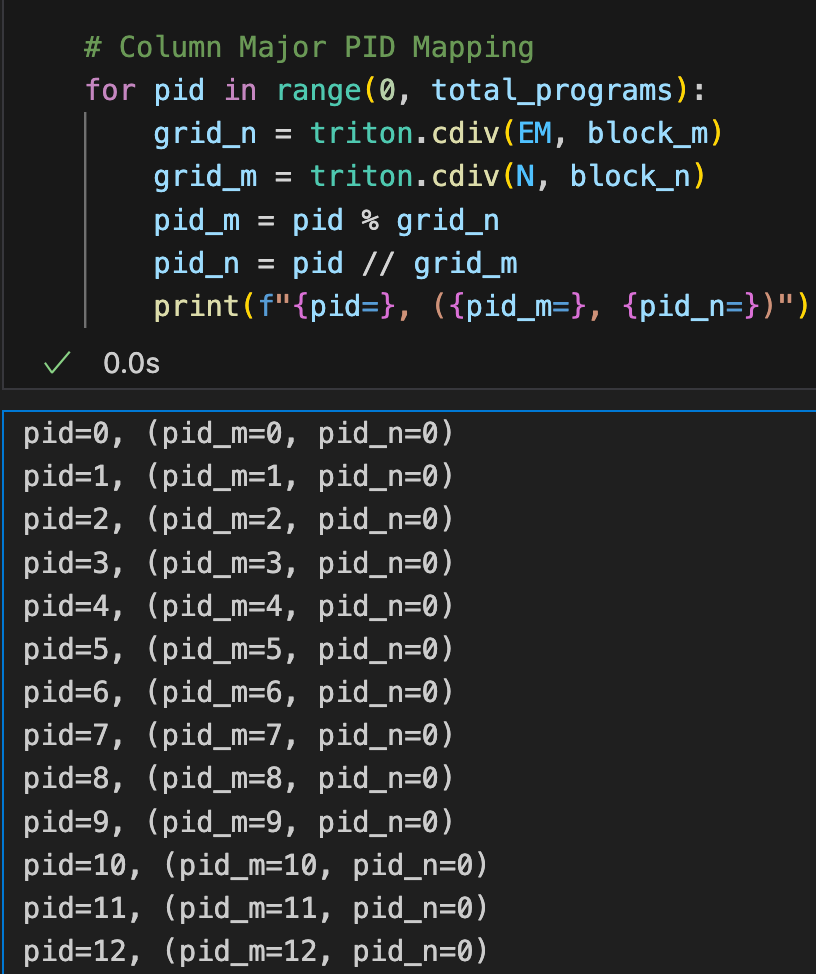
Figure 4. Column Major ordering in PyTorch
From above, we note that with this mapping, we schedule the GEMM such that we calculate the output blocks of C in the following order: C(0, 0), C(1, 0), C(2, 0),… etc. To understand the implications we provide the following illustration:
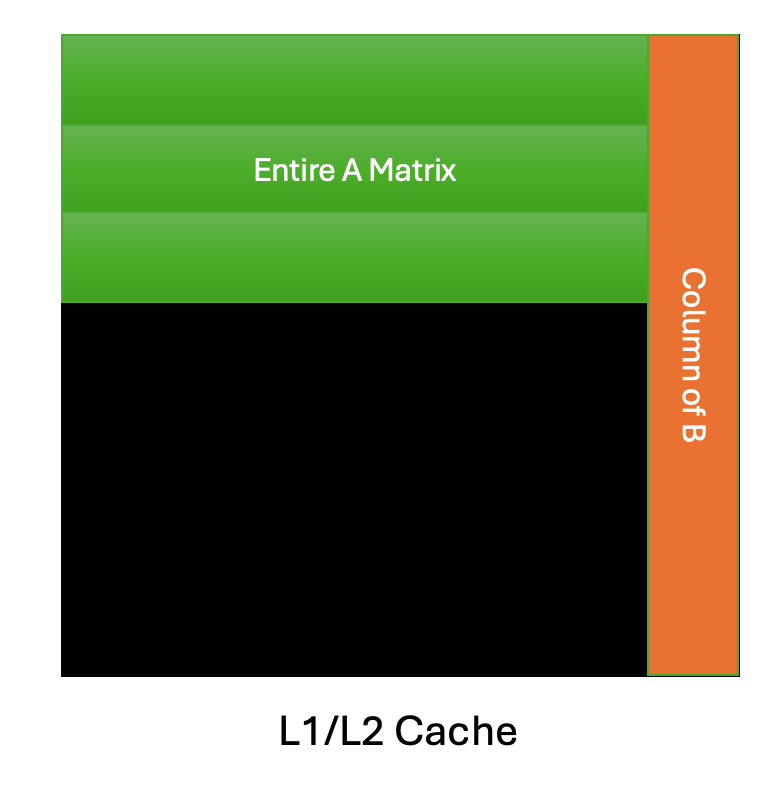
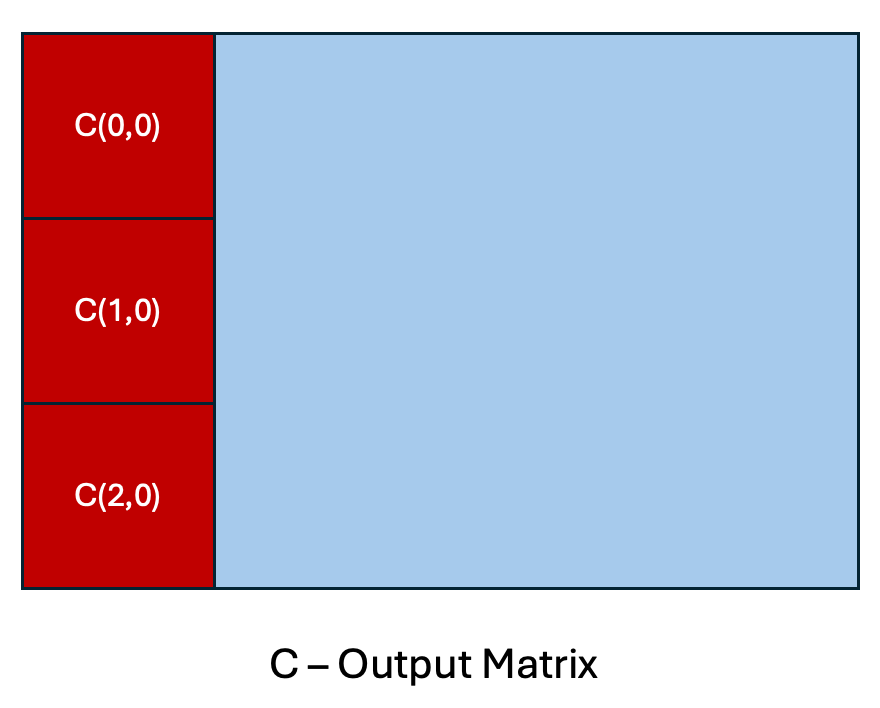
Figure 5. Cache Reuse Pattern for a Column-Major GEMM Schedule
In the above simplified view of a column-major schedule, let’s assume for a GEMM with skinny activation matrix A, that the entire matrix can fit in the GPU cache which is a reasonable assumption to make for the type of problem sizes we encounter in MoE inference. This allows for maximal reuse of the columns of the weight matrix B, due to the fact that the B column can be re-used for the corresponding output tile calculations, C(0,0), C(1, 0) and C(2, 0). Consider instead, a row-major schedule, C(0,0), C(0,1), C(0, 2) etc. We would have to evict the column of B, and issue multiple load instructions to DRAM to calculate the same amount of output blocks.
An important design consideration when optimizing kernels is a memory access pattern that results in the least amount of global load instructions. This optimal memory access pattern is achieved with the column-major schedule. The results below showcase the performance of the three schedules we investigated:
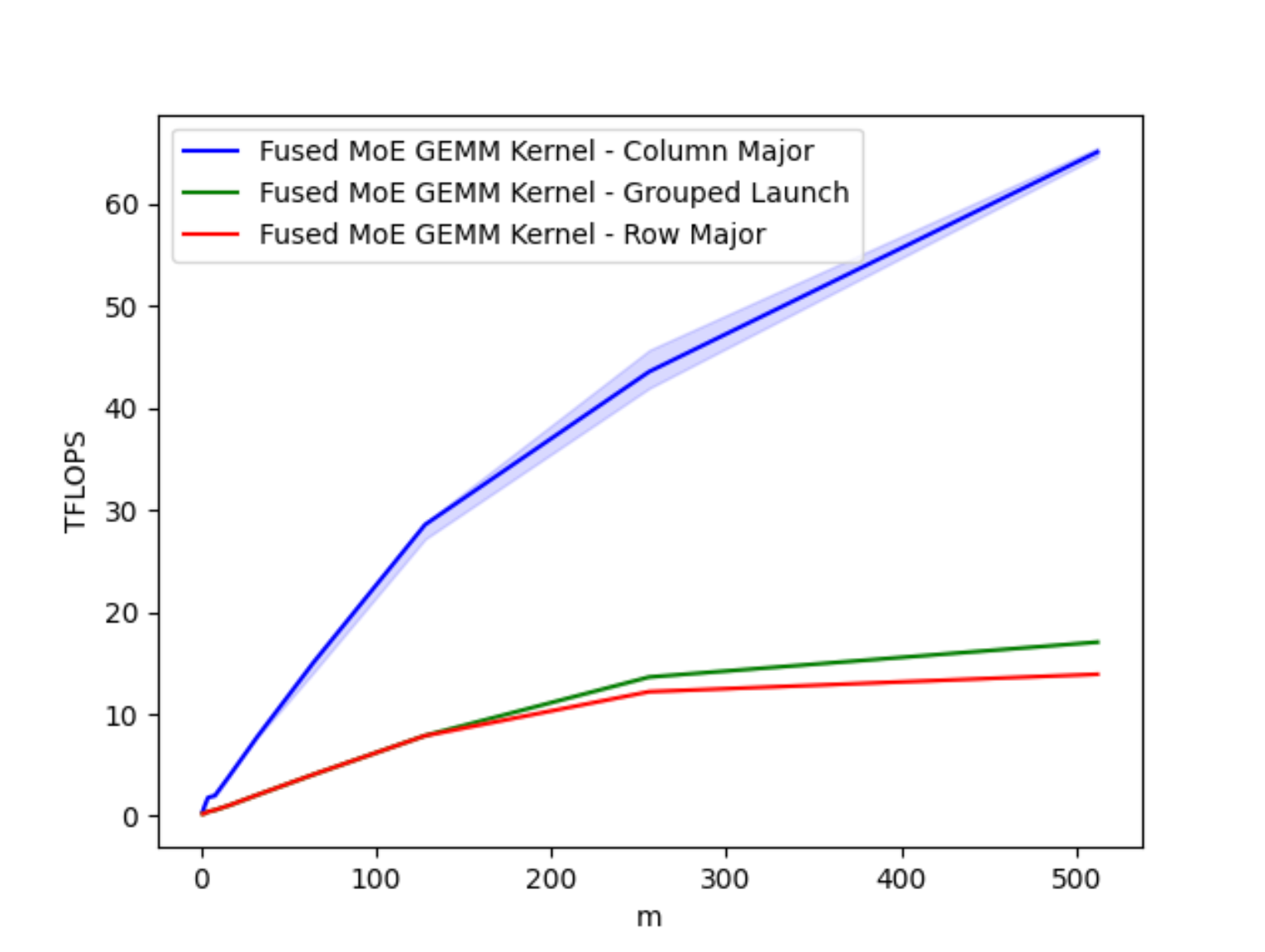
Figure 6. Comparison of GEMM Schedules on A100 for varying Batch Sizes M
The column-major schedule provides up to a 4x speedup over the other patterns, and as we’ll show in the next section, provides an optimal memory access pattern due to greatly improved data locality.
5.0 Nsight Compute Analysis – Throughput and Memory Access Pattern
For performance analysis, we focus on the M = 2 case for the H100. A similar study can be done for the A100 as many of the same observations carry over. We note the following salient results, that showcase the impact of our optimizations.
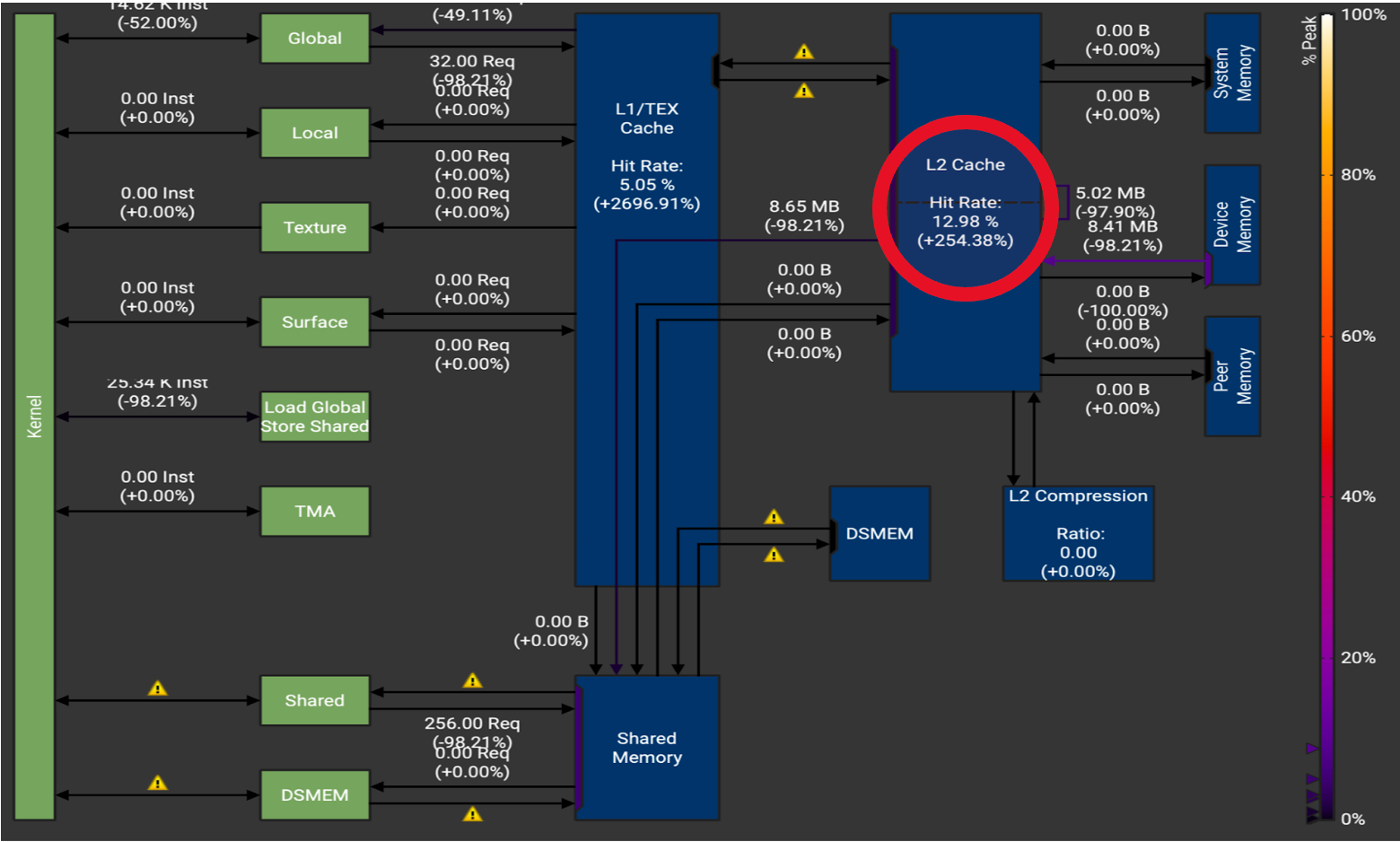
Figure 7. H100 Memory Throughput Chart for M = 2. Note the very large increase in the cache hit rates L1 cache hit rate (+2696%) and L2 cache hit rate (+254%).
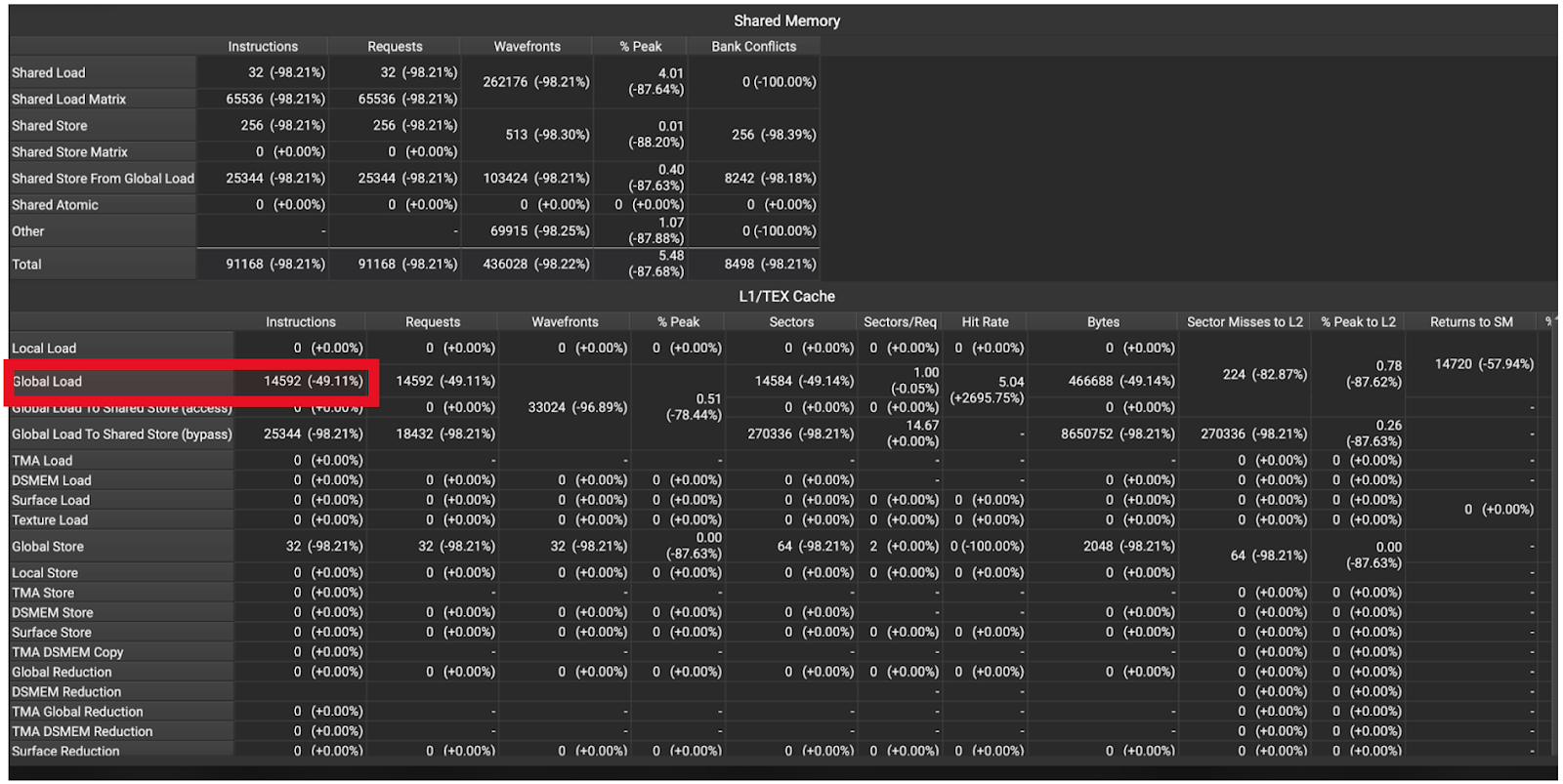
Figure 8. H100 Memory Instruction Statistics M = 2. Note the 49% reduction in global memory loads.
These statistics show that our optimizations had the intended effect, which can be seen in the reduced cache misses, reduced memory accesses and the resultant 2.7x speedup. More concretely, the trace shows us a 2.54x increase in L2 hit rate (Figure 7), and a ~50% reduction in DRAM accesses (Figure 8).
These improvements ultimately yield the reduced latency, with the optimized kernel being 2.7x faster for bs=2 and 4.4x for bs=512.
6.0 Future Work
Our kernel was tested in FP16, which showcases the numerics and performance of the column major scheduling for MoE, but most production models are using BFloat16. We encountered a limitation in Triton such that tl.atomic_add does not support Bfloat16 and hit launch latency concerns which would require cuda graph support for column major production use. In initial testing this translated to a 70% end-to-end speedup but, we encountered some expert mapping inconsistencies in an end to end environment that are not reflected in the test environment, so further work is needed to fully realize these speedups.
For future work, we intend to move this into a CUDA kernel which will ensure full BFloat16 support and reduced launch latency relative to Triton, and potentially resolve the expert routing inconsistency. We’ve also previously published work on enabling GPTQ W4A16 with Triton GEMM kernels, so natural follow-on work would include fusing dequantization into this kernel to allow for a GPTQ quantized inference path.
7.0 Reproducibility
We have open sourced the Triton kernel code along with an easy to run performance benchmark for readers interested in comparing or verifying the performance on their own GPU.
Acknowledgements
We want to thank Daniel Han, Raghu Ganti, Mudhakar Srivatsa, Bert Maher, Gregory Chanan, Eli Uriegas, and Geeta Chauhan for their review of the presented material and Woo Suk from the vLLM team as we built on his implementation of the Fused MoE kernel.
