Introduction
At the recent PyTorch Conference, Arm highlighted the widespread impact of its technology, spanning from cloud to edge, emphasizing its commitment to delivering its advanced AI computing capabilities seamlessly to millions of developers worldwide.

During the presentation, it was emphasized that Arm bears the immense responsibility of equipping 20+ million developers and billions of users with advanced AI computing features without friction. Achieving this requires crucial software collaborations across a vast ecosystem of software and hardware partners.
Just a few months ago, Arm launched Arm Kleidi, developer enablement technologies and resources to drive technical collaboration and innovation across the ML stack. This includes the KleidiAI software library providing optimized software routines, which when integrated into key frameworks such as XNNPACK enable automatic AI acceleration for developers on Arm Cortex-A CPUs.
Today, we’re excited to announce a new milestone for the AI open-source community that brings Arm even closer to realizing this vision: the integration of KleidiAI into ExecuTorch via XNNPACK, boosting AI workload performance on Arm mobile CPUs!
Thanks to the collaborative efforts of the engineering teams at Arm and Meta, AI developers can now deploy quantized Llama models which run up to 20% faster on Arm Cortex-A v9 CPUs with the i8mm ISA extension.
And there’s more exciting news – the ExecuTorch team has officially launched the Beta release!
This marks an important milestone in our partnership. In this blog, we are eager to share more details about ExecuTorch capabilities, the new Meta Llama 3.2 models, the integer 4-bit with per-block quantization, and the impressive performance recorded on certain Arm CPUs. Notably, we have achieved speeds of over 350 tokens per second on the prefill stage with the quantized Llama 3.2 1B model on Samsung S24+ device, as shown in the following screenshots.
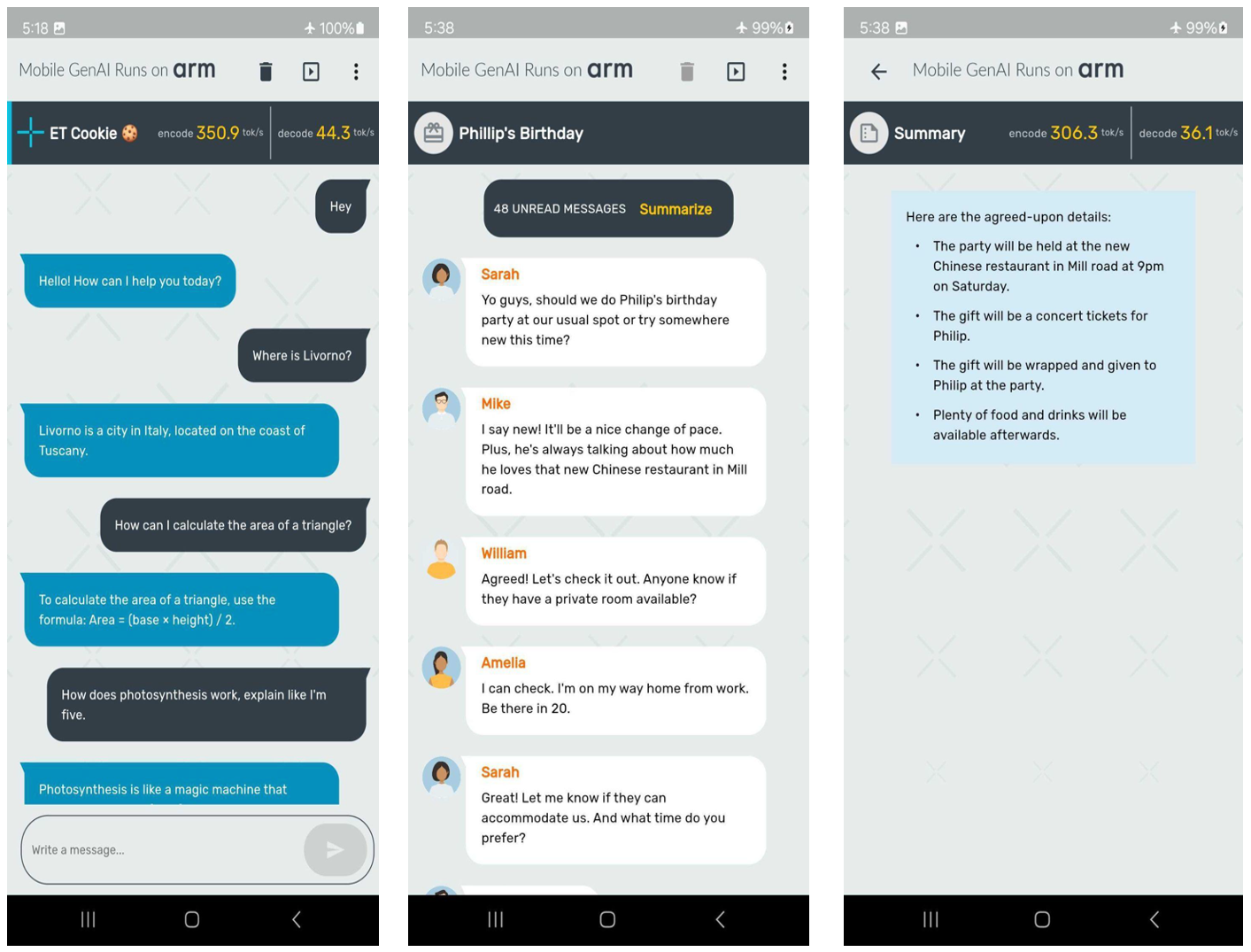
Now, let’s dive into the key components that enabled the demo creation presented in the preceding images. First up: new Llama 3.2 models!
Meta Llama 3.2
Meta recently announced the first lightweight quantized Llama models, which are designed to run on popular mobile devices. Meta used two techniques for quantizing Llama 3.2 1B and 3B models: Quantization-Aware Training (QAT) with LoRA adaptors (QLoRA), and SpinQuant, a state-of-the-art post-training quantization method. The quantized models were evaluated using PyTorch’s ExecuTorch framework as the inference engine, with the Arm CPU as a backend.
These instruction-tuned models retain the quality and safety of the original 1B and 3B models while achieving a 2-4x speedup and reducing model size by 56% on average and memory footprint by 41% on average compared to the original BF16 format.
In this blog post, we will demonstrate the performance improvements we observed in our experiments.
ExecuTorch
ExecuTorch is a PyTorch-native framework specifically designed for deploying AI models on-device, enhancing privacy and reducing latency. It supports the deployment of cutting-edge open-source AI models, including the Llama family of models and vision and speech models like Segment Anything and Seamless.
This unlocks new possibilities for edge devices such as mobile phones, smart glasses, VR headsets, and smart home cameras. Traditionally, deploying PyTorch-trained AI models to resource-limited edge devices has been challenging and time-consuming, often requiring conversion to other formats which could lead to errors and suboptimal performance. The varied toolchains across the hardware and edge ecosystem have also degraded the developer experience, making a universal solution impractical.
ExecuTorch addresses these issues by providing composable components that include core runtime, operator library, and delegation interface that allows for portability as well extensibility. Models can be exported using torch.export(), producing a graph that is natively compatible with the ExecuTorch runtime, capable of running on most edge devices with CPUs, and extendable to specialized hardware like GPUs and NPUs for enhanced performance.
Working with Arm, ExecuTorch now leverages the optimized low-bit matrix multiplication kernels from the Arm KleidiAI library to improve on-device Large Language Model (LLM) inference performance via XNNPACK. We also thank the XNNPACK team at Google for supporting this effort.
In this post, we will focus on this integration available in ExecuTorch
Evolving the architecture for AI workloads
At Arm, we have been deeply committed to investing in open-source projects and advancing new technologies in our processors since the early days of the deep learning wave, focusing on making AI workloads high-performing and more power-efficient.
For instance, Arm introduced the SDOT instruction, starting with the Armv8.2-A architecture, to accelerate dot product arithmetic between 8-bit integer vectors. This feature, now widely available in mobile devices, significantly speeds up the computation of quantized 8-bit models. After the SDOT instruction, Arm introduced the BF16 data type and the MMLA instruction to further enhance the floating-point and integer matrix multiplication performance on CPUs and, most recently, announced the Scalable Matrix Extension (SME), marking a significant leap forward in machine learning capabilities.
The following image shows a few examples of Arm CPU’s continuous innovations in the AI space over the last decade:

Given the widespread use of Arm CPUs, AI frameworks need to take full advantage of these technologies in key operators to maximize performance. Recognizing this, we saw the need for an open-source library to share these optimized software routines. However, we were mindful of the challenges in integrating a new library into AI frameworks, such as concerns about library size, dependencies, and documentation and the need to avoid adding extra burdens for developers. So, we took extra steps to gather feedback from our partners and ensure a smooth integration process that does not require additional dependencies for AI developers. This effort led to KleidiAI, an open-source library that provides optimized performance-critical routines for artificial intelligence (AI) workloads tailored for Arm CPUs. You can learn more about KleidiAI here.
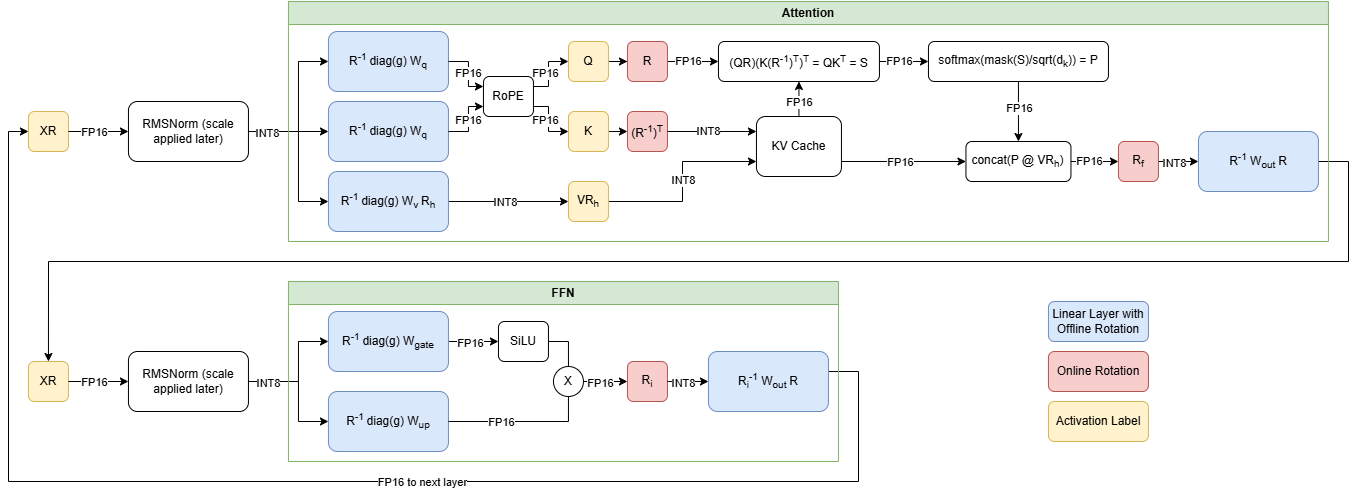
Working with the ExecuTorch team at Meta, Arm provided the software optimizations for their novel 4-bit with per-block quantization schema, which is used to accelerate the matrix multiplication kernel in the Transformer layer’s torch.nn.linear operator for Llama 3.2 quantized models. This flexible 4-bit quantization schema from ExecuTorch strikes a balance between model accuracy and low-bit matrix multiplication performance targeting on-device LLMs.
The integer 4-bit with per-block quantization
In KleidiAI, we introduced micro-kernels optimized for this new 4-bit integer quantization scheme (matmul_clamp_f32_qai8dxp_qsi4c32p)
As shown in the following image, this 4-bit quantization uses a per-block strategy for weight (RHS matrix) quantization and an 8-bit per-row quantization for activations (LHS matrix):
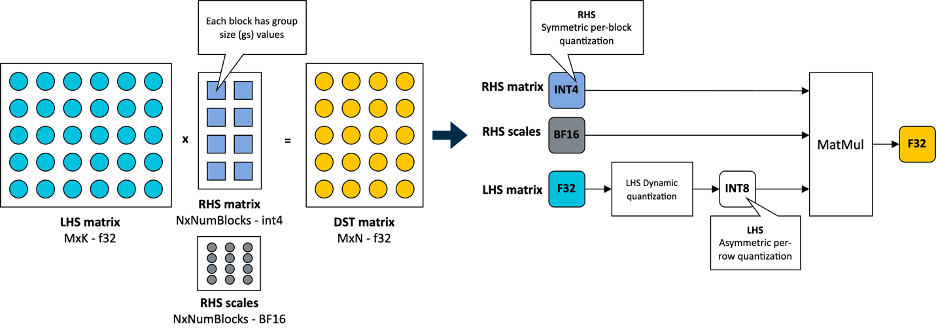
As you can see in the preceding image, each output feature map (OFM) in the weight matrix is divided into equally sized blocks (group size), with each block having a scale factor stored in BF16 format. BF16 is advantageous because it maintains the dynamic range of 32-bit floating-point (FP32) format with half the bit size, and it’s easy to convert to and from FP32 using a simple shift operation. This makes BF16 ideal for saving model space, preserving accuracy, and ensuring backward compatibility with devices that lack BF16 hardware acceleration. You can learn more about the BF16 format in this Arm Community blog post.
For completeness, this 4-bit quantization scheme and our implementation in KleidiAI allow users to configure group size for the linear weights (RHS), allowing them to trade-off between model size, model accuracy, and model performance if the model is quantized by the user.
At this point, we are ready to unveil the incredible performance recorded on Arm CPUs with ExecuTorch when running Llama 3.2 1B and Llama 3.2 3B. Let’s first go over metrics we will use to evaluate the performance of LLM inference.
Metrics for LLM Inference
Typically, performance metrics used to evaluate LLM performance during inference include:
- Time To First Token (TTFT): This measures the time it takes to produce the first output token after a prompt is provided by the user. This latency or response time is important for a good user experience, especially on a phone. TTFT is also a function of the length of the prompt or prompt tokens. To make this metric independent of the prompt length, we use Prefill tokens/second as a proxy here. The relationship between these is inverse: lower TTFT corresponds to higher Prefill tokens/second.
- Decode Performance: This is the average number of output tokens generated per second, thus reported in Tokens/Second. It is independent of the total number of tokens generated. For on-device inference, it is important to keep this higher than a user’s average reading speed.
- Peak Runtime Memory: This metric reflects the amount of RAM, typically reported in MegaBytes (MiB), needed to run the model with expected performance measured using the metrics above. Given the limited amount of RAM available on Android and iOS devices, this is one of the key metrics for on-device LLM deployment. It dictates the type of models that can be deployed on a device.
Results
The quantized Llama 3.2 1B models, both SpinQuant and QLoRA, are designed to run efficiently on a wide range of phones with limited RAM. In this section, we demonstrate that the quantized Llama 3.2 1B models can achieve over 350 tokens per second in the prefill phase and over 40 tokens per second in the decode stage. This level of performance is sufficient to enable on-device text summarization with a reasonable user experience using only Arm CPUs. To put this into perspective, on average, 50 unread messages contain about 600 tokens. With this performance, the response time (the time it takes for the first generated word to appear on the screen) is approximately two seconds.
We present measurements from a Samsung S24+ running vanilla Android. We used Llama 3.2 1B parameter models for these experiments. Although we only demonstrate using 1B models, similar performance gains can be expected for the 3B parameter models. The experiment setup involves doing a single warmup run, sequence length of 128, prompt length of 64, and using 6 out of 8 available CPUs, and measuring results over adb.
Using the ExecuTorch main branch from GitHub, we first generated the ExecuTorch PTE binary files for each model using the published checkpoints. Then, using the same repository, we generated the ExecuTorch runtime binary for Armv8. In the rest of the section, we will compare the performance of different quantized 1B models against the BF16 model using the binary built with KleidiAI. We will also compare the performance gains for quantized models between the binary with KleidiAI and the one without KleidiAI to distill the impact from KleidiAI.
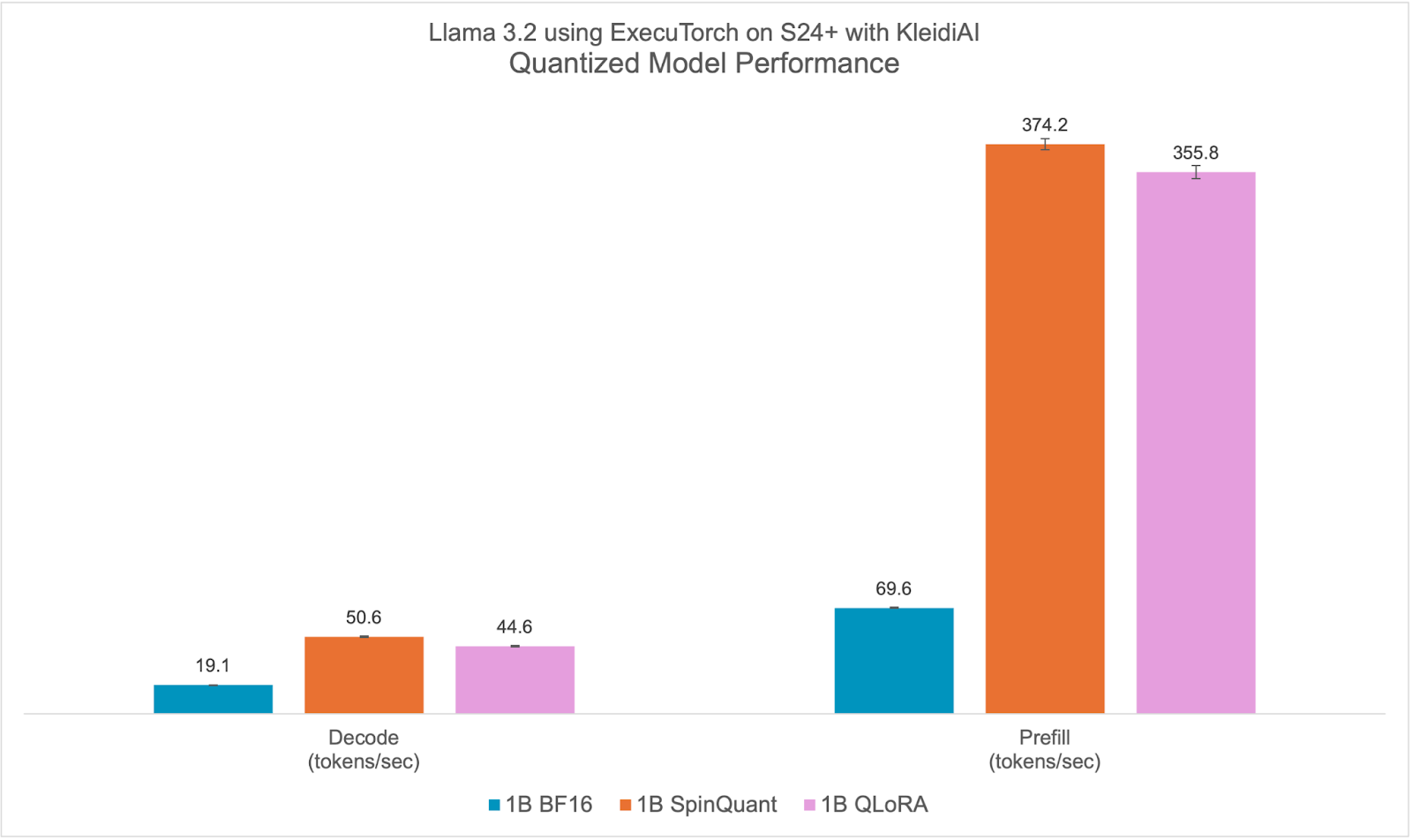
Quantized Model Performance
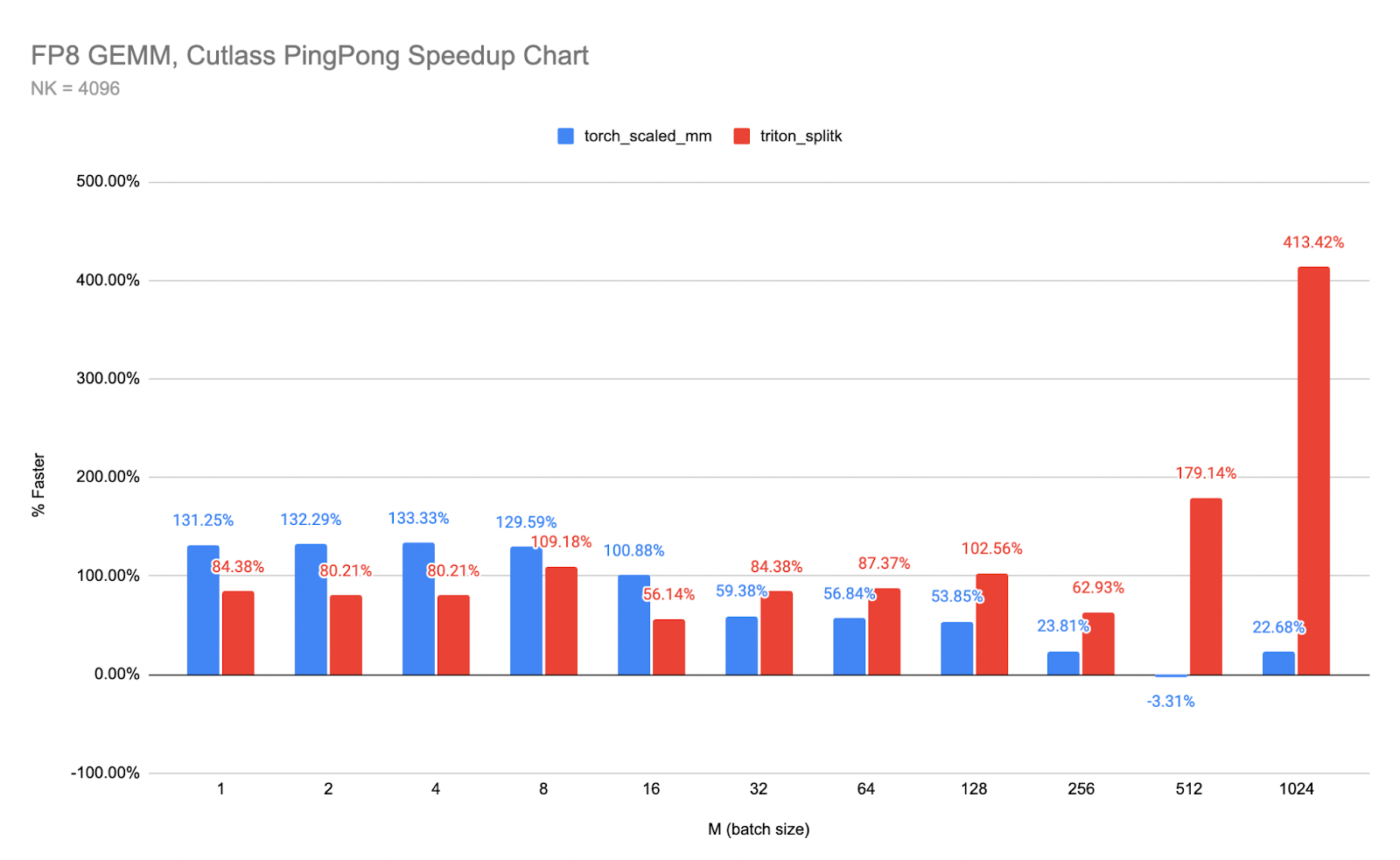
Llama 3.2 quantized models both SpinQuant and QLoRA perform significantly better on prompt prefill and text generation (decode) compared to the baseline BF16. We observed a >2x improvement in decode and a >5x improvement in prefill performance.
Furthermore, the quantized model size, PTE file size in bytes, is less than half that of the BF16 model, 2.3 GiB vs. 1.1 GiB. Although the size of int4 is a quarter of BF16, some layers in the model are quantized with int8, making the PTE file size ratio larger. We observed runtime peak memory footprint reduction of almost 40% from 3.1 GiB for the BF16 model to 1.9 GiB for the SpinQuant model, measured in Resident Set Size (RSS) for a maximum sequence length of 2048.
With all-around improvements, the new quantized Llama 3.2 models are ideal for on-device deployment targeting Arm CPUs. For more information on accuracy, check out the Meta Llama 3.2 blog.
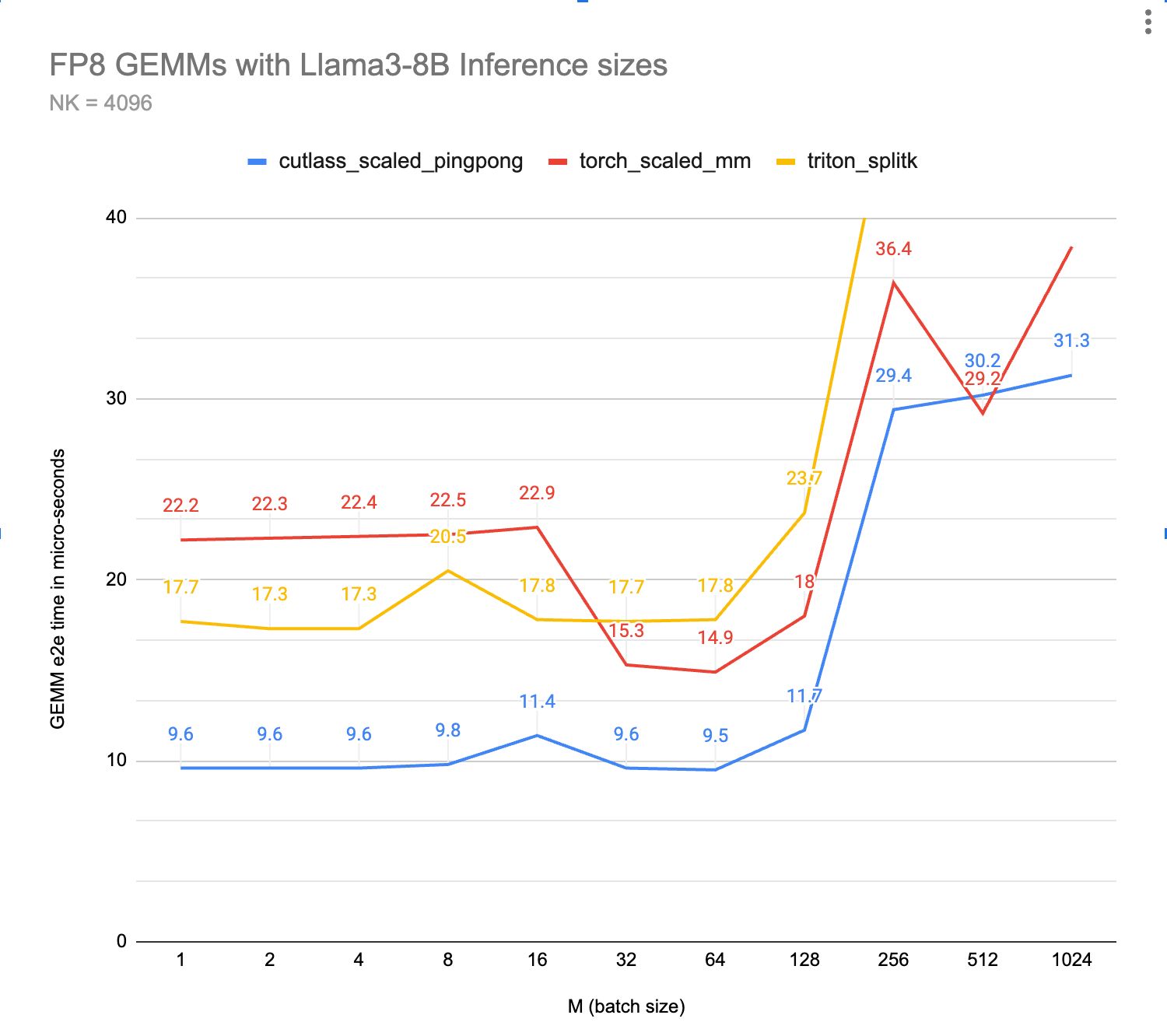
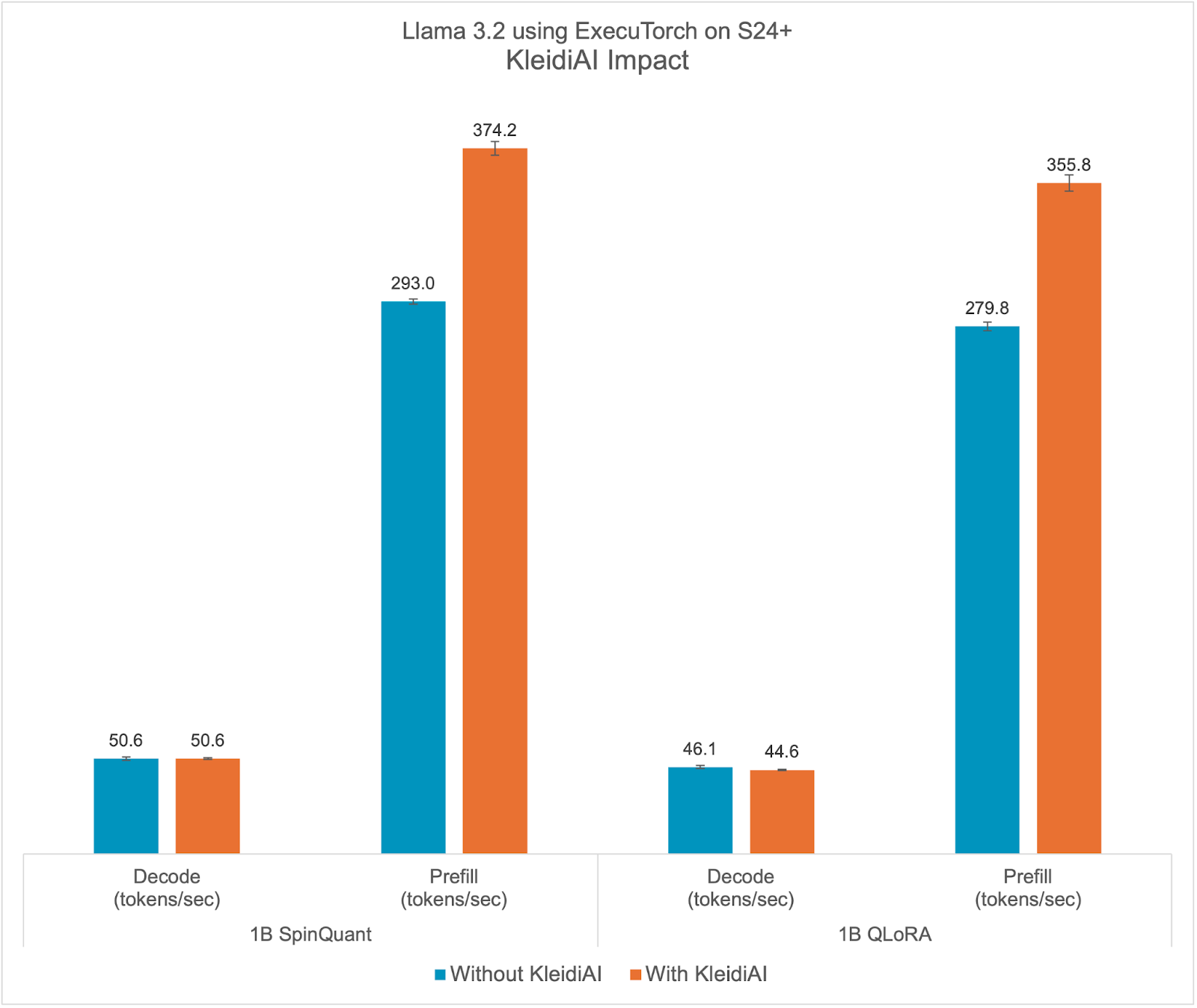
KleidiAI Impact
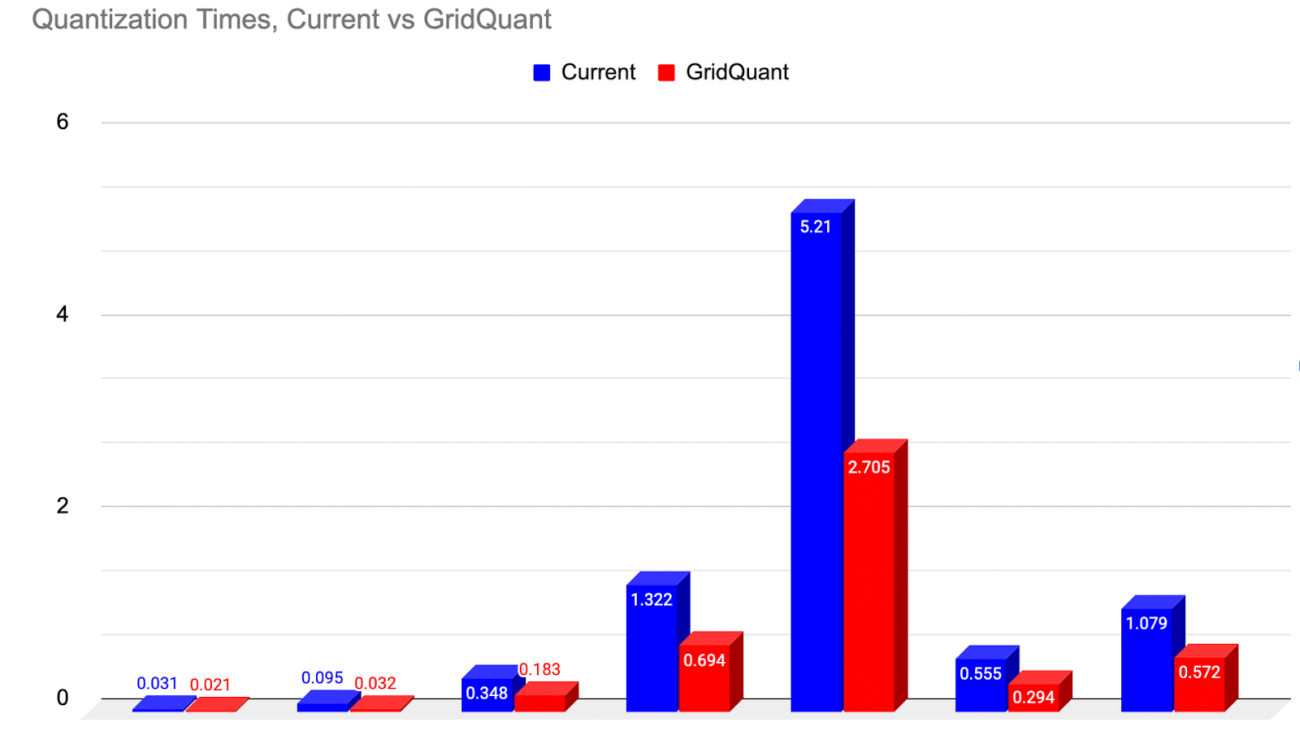
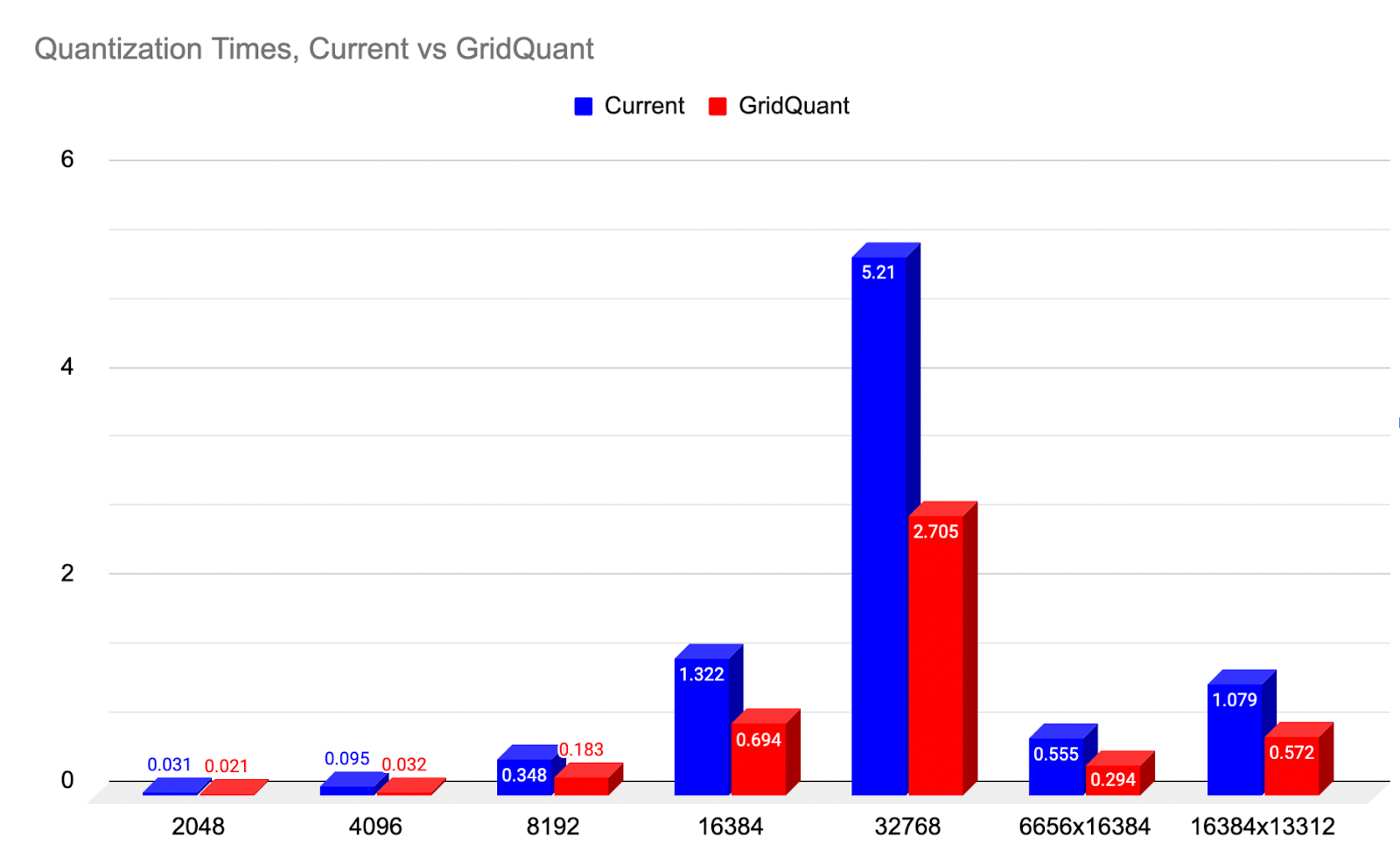
ExecuTorch relies on the Arm KleidiAI library to provide low-bit performant matrix multiplication kernels for the latest Arm CPUs with advanced Armv8/9 ISA features. These kernels are utilized for on-device quantized Llama 3.2 model inference in ExecuTorch. As depicted in the graph below, ExecuTorch achieves an average of >20% better prefill performance on S24+ with KleidiAI compared to non-KleidiAI kernels, while maintaining the same accuracy. This performance advantage is not limited to specific models or devices, and is expected to benefit all ExecuTorch models using low-bit quantized matrix multiplication on Arm CPUs.
To assess the impact of Kleidi, we generated two ExecuTorch runtime binaries targeting Arm Cortex-A CPUs and compared their performance.
- The first ExecuTorch runtime binary built with the Arm KleidiAI library through the XNNPACK library.
- The second binary was built without the Arm KleidiAI repository, using native kernels from the XNNPACK library.
Try it yourself!
Ready to experience the performance improvements firsthand? Here’s how you can try out ExecuTorch with the optimizations provided by KleidiAI on your projects: Here is a link to the learning path from Arm to start developing your own application using LLMs using ExecuTorch and KleidiAI.
We look forward to hearing your feedback!
Read More