Fig. 1: The central hypothesis: within a dataset with finite samples, there are correlations between the high-frequency component and the “semantic” component of the images. As a result, the model will perceive both the high-frequency component as well as the “semantic” ones, leading to generalization behavior counterintuitive to humans.
It’s all about data
There are many works aiming to explain the generalization behavior of neural networks using heavy mathematical machinery, but we will do something different here: with a simple and intuitive twist of data, we will show that many generalization mysteries (like adversarial vulnerability, BatchNorm’s efficacy, and the “generalization paradox”) might be results of our overconfidence in processing data through naked eyes. Or simply:
The models may have not outsmarted us, but the data has.
Let’s start with an interesting observation (Fig. 2): we trained a ResNet-18 with the Cifar10 dataset, picked a test sample, and plotted the model’s prediction confidence for this sample. Then we mapped the sample into the frequency domain through Fourier transform, and cut the frequency representation into its high-frequency component (HFC) and low-frequency component (LFC). We reconstructed the image through these two components and fed the reconstructed image into the model:
- HFC-reconstructed images look distinctly different from the original sample but predicted to be the same label.
- LFC-reconstructed images look similar to the original sample but the model classifies them differently.
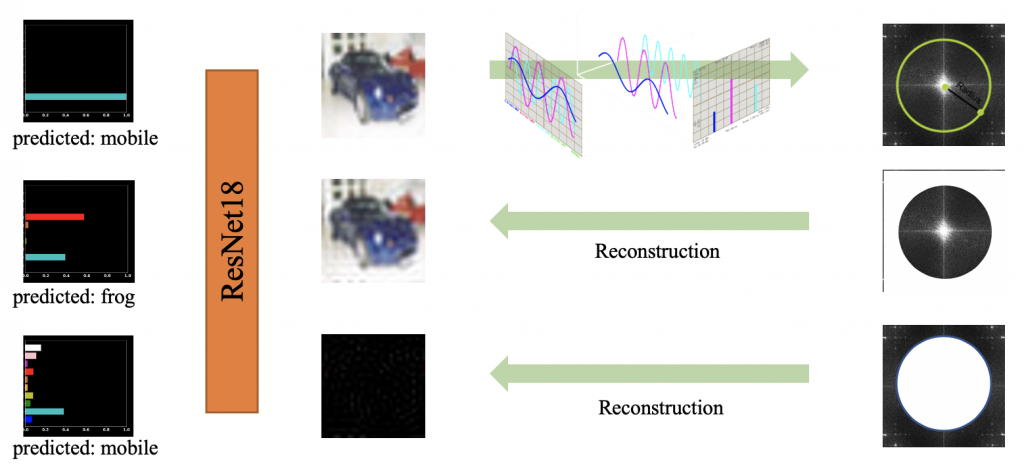
Although this phenomenon can only be observed with a subset of samples (~600 images), it’s striking enough to raise an alarm.
Why does a model behave like this?
We believe the underlying reason is the coincidental correlation between HFC and the “semantics” depicted within a dataset (Fig. 1). With a finite number of samples from the same distribution, chances are that the human-imperceptible HFC is correlated with how a human annotates the image; thus, when a model is optimized to reduce the training loss, it can pick up either the “semantics” or HFC to reduce the loss, leading to high prediction accuracy even though the model may not truly “understand” the data.
Please note: we are not claiming that the model itself has a tendency to capture HFC. Instead, our main argument is that a generic model does not have the incentive to learn LFC only; thus, it may end up learning a mixture of LFC and HFC.
Also, one may wonder whether the fact that models can capture HFC is promising or worrisome. One side may argue that this enables the development of models that can surpass humans on the test data (likely only when the test data is from the same distribution as the training data), while the other side may argue that the resulting models, despite performing better on test data from the same distribution, may underperform after deployed on similar data from other distributions (i.e., HFC may be dataset-specific). This post does not intend to resolve this argument, but only to offer the observations we made.
Observations
We can leverage the main observation to help explain multiple previously elusive empirical phenomena. In this post, we will highlight two discussions from our paper.
One of the roots of adversarial vulnerability
Conceptually similar to the argument made in a preceding paper, we show that the predictive signal from HFC is one of the roots of adversarial vulnerability. However, in contrast to this prior work, we offer a concrete proposal regarding what the adversarial features might be: signals from HFC.
To investigate the relationship, we trained an adversarially robust model with Madry’s adversarial training method and studied the convolutional kernels of a robust model and a vanilla model. We notice that the convolutional kernels of a robust model tend to be smoother (“smooth” in the sense that differences between adjacent values are small), as shown in Fig. 3. Relevant mathematical tools suggest that smooth convolutional kernels only consider a negligible amount of HFC in data, thus linking HFC to adversarial vulnerability.

With this knowledge, a more enticing question is whether we can directly smooth a vanilla model’s convolutional kernel to improve its adversarial robustness. To answer this question, we tested multiple methods to smooth convolutional kernels:
- To heuristically adjust the weights of trained kernels to improve the smoothness.
- To filter out the high-frequency information of trained kernels (not reported in our paper).
- To design regularization schemes limiting the differences of adjacent values of kernels during training (not reported in our paper).
Unfortunately, only marginal improvements are observed. Thus, we can conclude that adversarially robust models tend to have smooth convolutional kernels, but the inverse is not necessarily true. In other words, HFC is one of the issues of adversarial vulnerability, but not all of the issues.
However, one solution inspired by this observation can indeed defend against most adversarial attacks at a remarkable rate:
- To filter out HFC of input images before feeding the data into models.
The method can improve the robustness of a model, but the method is effectively masking the gradient of the model, thus not solving the adversarial attack & defense problem the research community focuses on.
The Efficacy of BatchNormalization
Another interesting observation concerns the efficacy of BatchNorm. BatchNorm is one of the most effective training heuristics in modern deep learning research, especially in computer vision applications. However, why BatchNorm can help training so significantly is not yet well understood. Interestingly, our experiments offer another perspective on why BatchNorm often helps.
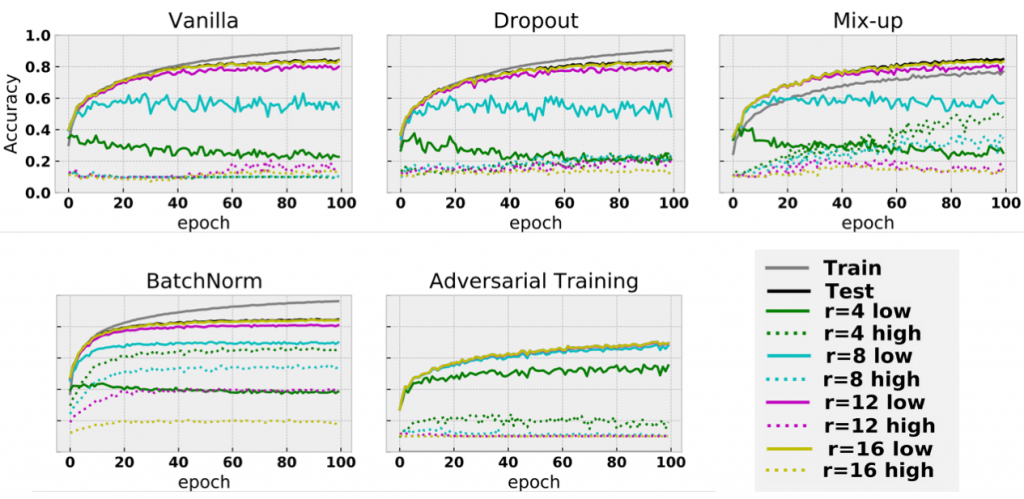
In Fig. 4, along with the increment of training epochs, we report the accuracies of training data and various copies of test data, where r refers to the radius we used to cut LFC and HFC, and solid/dashed line denotes the performances from LFC/HFC, respectively. Thus, the higher the curves get in dashed lines, the more HFC a model takes advantage of.
Surprisingly, the model trained with BatchNorm exploits a significant amount of HFC, as the dashed curves of the 4th panel are remarkably higher than those of the other panels. This observation suggests that one of the reasons why BatchNorm helps is that it encourages the usage of HFC. As we argued previously, there are multiple predictive signals (LFC and HFC) in the data. It is expected that the more signals a model uses, the higher test accuracy a model can get, consistent with the fact that BatchNorm is widely known as a method to improve testing accuracy.
Intuitively, we conjecture that the performance boost is due to the fact that HFC usually only involves pixels with very small magnitude (as the reconstructed images look mostly black to humans). BatchNorm conveniently rescales these signals through normalization, thus leading to improved accuracy.
One may naturally wonder what our observation implies regarding the usage of BatchNorm: we suggest that we might need to reevaluate the value of BatchNorm, especially for models to meet the expectations of being robust in multiple datasets. Our observation also conveniently aligns with another observation suggesting that BatchNorm may encourage adversarial vulnerability.
In our paper, we also have discussions relating to the paradox widely known as “rethinking generalization”, formal results on the tradeoff between accuracy and robustness, and experiments suggesting that these interesting phenomena may appear in other vision tasks such as object detection.
Conclusions
For more information, please refer to our paper, where we mainly draw three conclusions:
- Since HFC may be dataset-specific, SOTA (state-of-the-art) may not be as important as the community thought; the alignment between human and the models may be more important.
- We may need a new testing regime for computer vision; for example, a simple way is to always test the models over LFC-reconstructed images in addition to the original testing images.
- Explicit inductive bias design to align the models and the human may play an important role.
Relevant resources:
- Manuscript, accepted at CVPR 2020 as an oral.
- Codes to replicate the main results.
- Poster used for the conference presentation.
- If one is interested in more relevant discussions, here is a brief overview of trustworthy machine learning, serving as a lecture of CMU 10708 PGM course in 2020.
DISCLAIMER: All opinions expressed in this post are those of the author and do not represent the views of CMU.
