Sparse models stand out among the most promising approaches for the future of deep learning. Instead of every part of a model processing every input (“dense” modeling), sparse models employing conditional computation learn to route individual inputs to different “experts” in a potentially huge network. This has many benefits. First, model size can increase while keeping computational cost constant — an effective and environmentally friendlier way to scale models, which is often key to high performance. Sparsity also naturally compartmentalizes neural networks. Dense models that learn many different tasks simultaneously (multitask) or sequentially (continual learning) often suffer negative interference, where too much task variety means it is better to just train one model per task, or catastrophic forgetting, where the model becomes worse at earlier tasks as new ones are added. Sparse models help avoid both these phenomena — by not applying the whole model to all inputs, “experts” in the model can specialize on different tasks or data types while still taking advantage of shared parts of the model.
Research on sparsity has long been pursued at Google Research. Pathways summarizes the research vision of building one single large model that diligently handles thousands of tasks and numerous data modalities. So far there has been considerable progress in sparse unimodal models for language (Switch, Task-MoE, GLaM) and computer vision (Vision MoE). Today, we take another important step towards the Pathways vision by studying large sparse models that simultaneously handle images and text with modality-agnostic routing. A relevant approach is multimodal contrastive learning, which requires a solid understanding of both images and text in order to align pictures with their correct text description. The strongest models that tackle this task to date rely on independent networks for each modality (a “two-tower” approach).
In “Multimodal Contrastive Learning with LIMoE: the Language Image Mixture of Experts”, we present the first large-scale multimodal architecture using a sparse mixture of experts. It simultaneously processes both images and text, but uses sparsely activated experts that naturally specialize. On zero-shot image classification, LIMoE outperforms both comparable dense multimodal models and two-tower approaches. The largest LIMoE achieves 84.1% zero-shot ImageNet accuracy, comparable to more expensive state-of-the-art models. Sparsity enables LIMoE to scale up gracefully and learn to handle very different inputs, addressing the tension between being a jack-of-all-trades generalist and a master-of-one specialist.
Sparse Mixture of Expert Models
Transformers represent data as a sequence of vectors (or tokens). Though originally developed for text, they can be applied to most things that are representable as a sequence of tokens, e.g., images, videos, and audio. Recent large-scale MoE models add expert layers to the Transformer architecture (e.g., gShard and ST-MoE in natural language processing, and Vision MoE for vision tasks).
A standard Transformer consists of many “blocks”, each containing various different layers. One of these layers is a feed-forward network (FFN). For LIMoE and the works cited above, this single FFN is replaced by an expert layer that contains many parallel FFNs, each of which is an expert. Given a sequence of tokens to process, a simple router learns to predict which experts should handle which tokens. Only a small number of experts are activated per token, meaning although the model capacity is significantly increased by virtue of having so many experts, the actual computational cost is controlled by using them sparsely. If only one expert is activated, the model’s cost is roughly equivalent to the standard Transformer model.
LIMoE does precisely that, activating one expert per example, thereby matching the computational cost of the dense baselines. What’s different is that the LIMoE router might see tokens of either image or text data.
A unique failure mode of MoE models occurs when they try to send all tokens to the same expert. Typically this is addressed with auxiliary losses, extra training objectives that encourage balanced expert usage. We found that dealing with multiple modalities interacted with sparsity to cause new failure modes that existing auxiliary losses could not address. To overcome this, we developed new auxiliary losses (more details in the paper) and used routing prioritization (BPR) during training, two innovations that resulted in stable and high performance multimodal models.
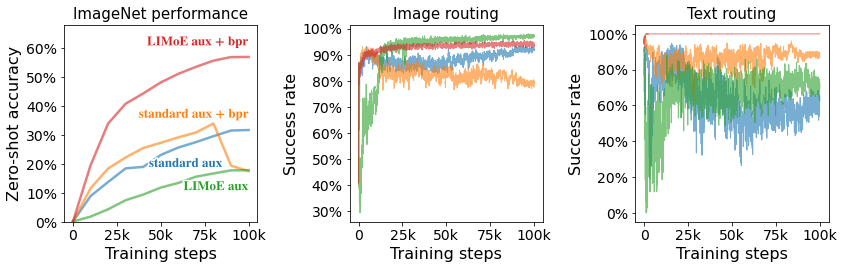 |
| The new auxiliary losses (LIMoE aux) and routing prioritization (BPR) stabilized and improved overall performance (left) and increased the success rate of routing behavior (middle and right). A low success rate means the router does not use all the experts available and drops many tokens due to individual expert capacity being reached, which usually indicates the sparse model is not learning well. The combination introduced for LIMoE ensures high routing success rates for both images and text and consequently leads to significantly better performance. |
Contrastive Learning with LIMoE
In multimodal contrastive learning, models are trained on paired image-text data (e.g., a photo and its caption). Typically, an image model extracts a representation of images, and a different text model extracts a representation of text. The contrastive learning objective encourages the image and text representations to be close for the same image-text pair and far away for content from different pairs. Such models with aligned representations can be adapted to new tasks without extra training data (“zero-shot”), e.g., an image will be classified as a dog if its representation is closer to the representation of the word “dog” than the word “cat”. This idea scales to thousands of classes and is referred to as zero-shot image classification.
CLIP and ALIGN (both two-tower models) scaled this process to achieve 76.2% and 76.4% zero-shot classification accuracy on the popular ImageNet dataset. We study one-tower models which compute both image and text representations. We find this reduces performance for dense models, likely due to negative interference or insufficient capacity. However, a compute-matched LIMoE not only improves over the one-tower dense model, but also outperforms two-tower dense models. We trained a series of models in a comparable training regimen to CLIP. Our dense L/16 model achieves 73.5% zero-shot accuracy, whereas LIMoE-L/16 gets to 78.6%, even outperforming CLIP’s more expensive, two-tower L/14 model (76.2%). As shown below, LIMoE’s use of sparsity provides a remarkable performance boost over dense models with equivalent cost.
 |
| For a given compute cost (x-axis), LIMoE models (circles, solid line) are significantly better than their dense baselines (triangles, dashed line). The architecture indicates the size of the underlying transformer, increasing from left (S/32) to right (L/16). Following standard convention, S (small), B (base), and L (large) refer to model scale. The number refers to the patch size, where smaller patches imply a larger architecture. |
LiT and BASIC pushed zero-shot accuracy for dense two-tower models to 84.5% and 85.6% respectively. In addition to scaling, these approaches made use of specialized pre-training methods, repurposing image models that were already of exceptionally high quality. LIMoE-H/14 does not benefit from any pre-training or modality-specific components, but still achieved a comparable 84.1% zero-shot accuracy training from scratch. The scale of these models is also interesting to compare: LiT and BASIC are 2.1B and 3B parameter models. LIMoE-H/14 has 5.6B parameters in total, but via sparsity it only applies 675M parameters per token making it significantly more lightweight.
| Data seen during training | |||||
| Model | Pre-training | Image-text | Total | Parameters per token | ImageNet accuracy |
| CLIP | – | 12.8B | 12.8B | ~200M | 76.2% |
| ALIGN | – | 19.8B | 19.8B | ~410M | 76.4% |
| LiT | 25.8B | 18.2B | 44.0B | 1.1B | 84.5% |
| BASIC | 19.7B | 32.8B | 52.5B | 1.5B | 85.6% |
| LIMoE H/14 | – | 23.3B | 23.3B | 675M | 84.1% |
Understanding LIMoE’s Behavior
LIMoE was motivated by the intuition that sparse conditional computation enables a generalist multimodal model to still develop the specialization needed to excel at understanding each modality. We analyzed LIMoE’s expert layers and uncovered a few interesting phenomena.
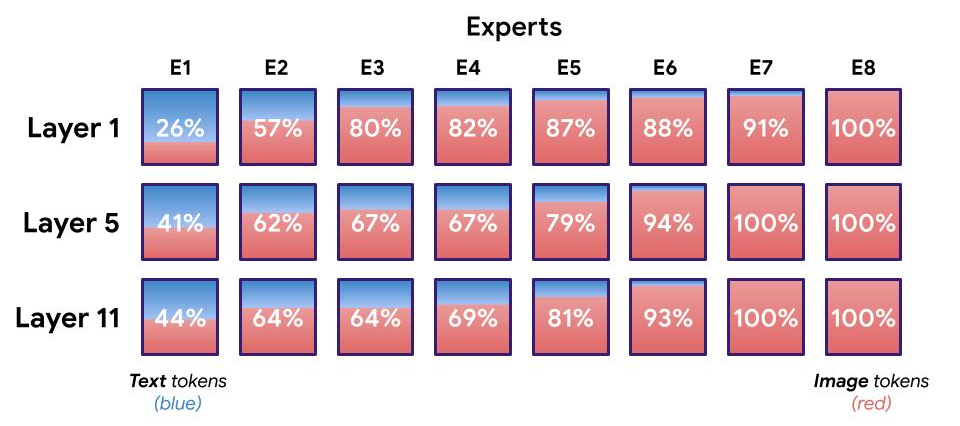
First, we see the emergence of modality-specialized experts. In our training setup there are many more image tokens than text tokens, so all experts tend to process at least some images, but some experts process either mostly images, mostly text, or both.
There are also some clear qualitative patterns among the image experts — e.g., in most LIMoE models, there is an expert that processes all image patches that contain text. In the example below, one expert processes fauna and greenery, and another processes human hands.
Moving Forward
Multimodal models that handle many tasks are a promising route forward, and there are two key ingredients for success: scale, and the ability to avoid interference between distinct tasks and modalities while taking advantage of synergies. Sparse conditional computation is an excellent way of doing both. It enables performant and efficient generalist models that also have the capacity and flexibility for the specialization necessary to excel at individual tasks, as demonstrated by LIMoE’s solid performance with less compute.
Acknowledgements
We thank our co-authors on this work: Joan Puigcerver, Rodolphe Jenatton and Neil Houlsby. We also thank Andreas Steiner, Xiao Wang and Xiaohua Zhai, who led early explorations into dense single-tower models for contrastive multimodal learning, and also were instrumental in providing data access. We enjoyed useful discussions with André Susano Pinto, Maxim Neumann, Barret Zoph, Liam Fedus, Wei Han and Josip Djolonga. Finally, we would also like to thank and acknowledge Tom Small for the awesome animated figure used in this post.