Bayesian optimization (BayesOpt) is a powerful tool widely used for global optimization tasks, such as hyperparameter tuning, protein engineering, synthetic chemistry, robot learning, and even baking cookies. BayesOpt is a great strategy for these problems because they all involve optimizing black-box functions that are expensive to evaluate. A black-box function’s underlying mapping from inputs (configurations of the thing we want to optimize) to outputs (a measure of performance) is unknown. However, we can attempt to understand its internal workings by evaluating the function for different combinations of inputs. Because each evaluation can be computationally expensive, we need to find the best inputs in as few evaluations as possible. BayesOpt works by repeatedly constructing a surrogate model of the black-box function and strategically evaluating the function at the most promising or informative input location, given the information observed so far.
Gaussian processes are popular surrogate models for BayesOpt because they are easy to use, can be updated with new data, and provide a confidence level about each of their predictions. The Gaussian process model constructs a probability distribution over possible functions. This distribution is specified by a mean function (what these possible functions look like on average) and a kernel function (how much these functions can vary across inputs). The performance of BayesOpt depends on whether the confidence intervals predicted by the surrogate model contain the black-box function. Traditionally, experts use domain knowledge to quantitatively define the mean and kernel parameters (e.g., the range or smoothness of the black-box function) to express their expectations about what the black-box function should look like. However, for many real-world applications like hyperparameter tuning, it is very difficult to understand the landscapes of the tuning objectives. Even for experts with relevant experience, it can be challenging to narrow down appropriate model parameters.
In “Pre-trained Gaussian processes for Bayesian optimization”, we consider the challenge of hyperparameter optimization for deep neural networks using BayesOpt. We propose Hyper BayesOpt (HyperBO), a highly customizable interface with an algorithm that removes the need for quantifying model parameters for Gaussian processes in BayesOpt. For new optimization problems, experts can simply select previous tasks that are relevant to the current task they are trying to solve. HyperBO pre-trains a Gaussian process model on data from those selected tasks, and automatically defines the model parameters before running BayesOpt. HyperBO enjoys theoretical guarantees on the alignment between the pre-trained model and the ground truth, as well as the quality of its solutions for black-box optimization. We share strong results of HyperBO both on our new tuning benchmarks for near–state-of-the-art deep learning models and classic multi-task black-box optimization benchmarks (HPO-B). We also demonstrate that HyperBO is robust to the selection of relevant tasks and has low requirements on the amount of data and tasks for pre-training.
 |
| In the traditional BayesOpt interface, experts need to carefully select the mean and kernel parameters for a Gaussian process model. HyperBO replaces this manual specification with a selection of related tasks, making Bayesian optimization easier to use. The selected tasks are used for pre-training, where we optimize a Gaussian process such that it can gradually generate functions that are similar to the functions corresponding to those selected tasks. The similarity manifests in individual function values and variations of function values across the inputs. |
Loss functions for pre-training
We pre-train a Gaussian process model by minimizing the Kullback–Leibler divergence (a commonly used divergence) between the ground truth model and the pre-trained model. Since the ground truth model is unknown, we cannot directly compute this loss function. To solve for this, we introduce two data-driven approximations: (1) Empirical Kullback–Leibler divergence (EKL), which is the divergence between an empirical estimate of the ground truth model and the pre-trained model; (2) Negative log likelihood (NLL), which is the the sum of negative log likelihoods of the pre-trained model for all training functions. The computational cost of EKL or NLL scales linearly with the number of training functions. Moreover, stochastic gradient–based methods like Adam can be employed to optimize the loss functions, which further lowers the cost of computation. In well-controlled environments, optimizing EKL and NLL lead to the same result, but their optimization landscapes can be very different. For example, in the simplest case where the function only has one possible input, its Gaussian process model becomes a Gaussian distribution, described by the mean (m) and variance (s). Hence the loss function only has those two parameters, m and s, and we can visualize EKL and NLL as follows:
 |
| We simulate the loss landscapes of EKL (left) and NLL (right) for a simple model with parameters m and s. The colors represent a heatmap of the EKL or NLL values, where red corresponds to higher values and blue denotes lower values. These two loss landscapes are very different, but they both aim to match the pre-trained model with the ground truth model. |
Pre-training improves Bayesian optimization
In the BayesOpt algorithm, decisions on where to evaluate the black-box function are made iteratively. The decision criteria are based on the confidence levels provided by the Gaussian process, which are updated in each iteration by conditioning on previous data points acquired by BayesOpt. Intuitively, the updated confidence levels should be just right: not overly confident or too unsure, since in either of these two cases, BayesOpt cannot make the decisions that can match what an expert would do.
In HyperBO, we replace the hand-specified model in traditional BayesOpt with the pre-trained Gaussian process. Under mild conditions and with enough training functions, we can mathematically verify good theoretical properties of HyperBO: (1) Alignment: the pre-trained Gaussian process guarantees to be close to the ground truth model when both are conditioned on observed data points; (2) Optimality: HyperBO guarantees to find a near-optimal solution to the black-box optimization problem for any functions distributed according to the unknown ground truth Gaussian process.
 |
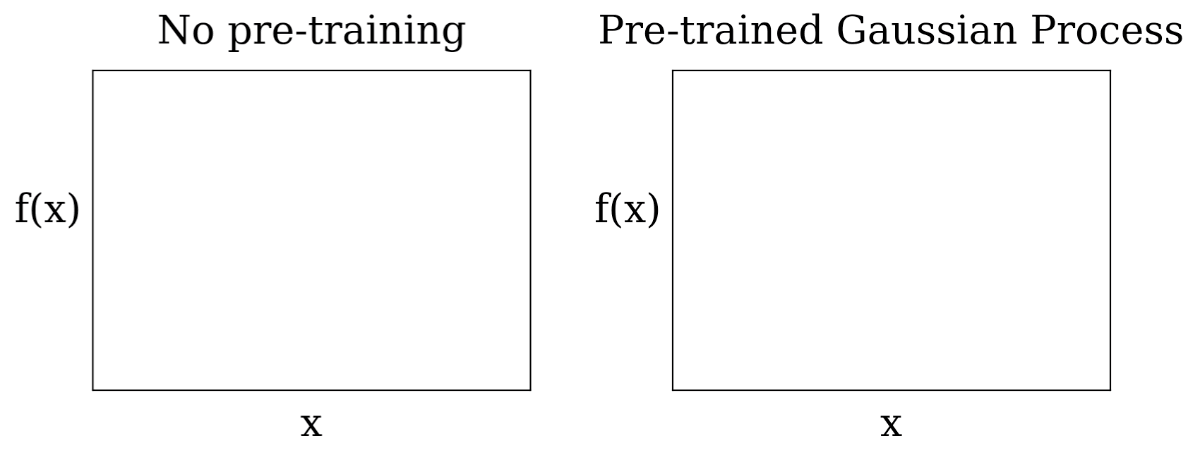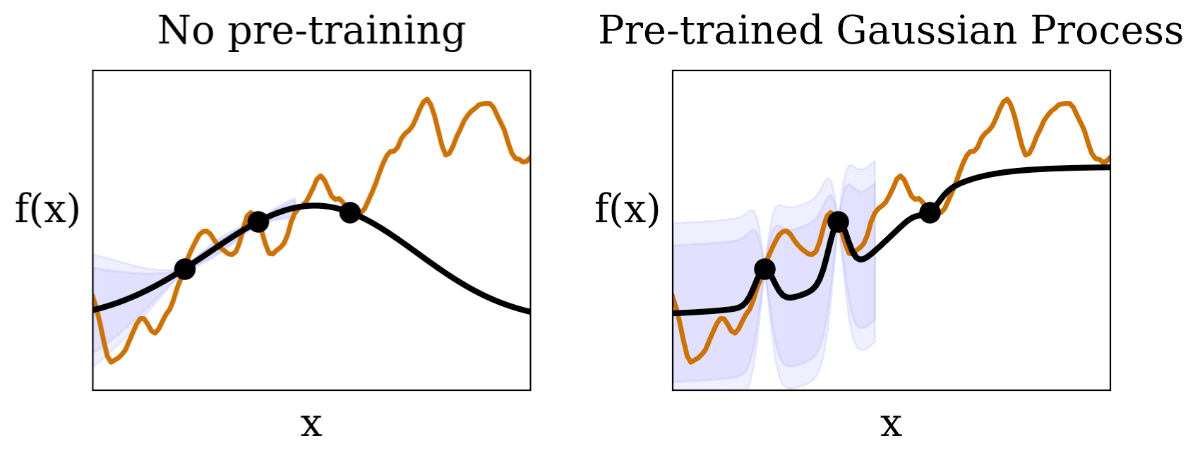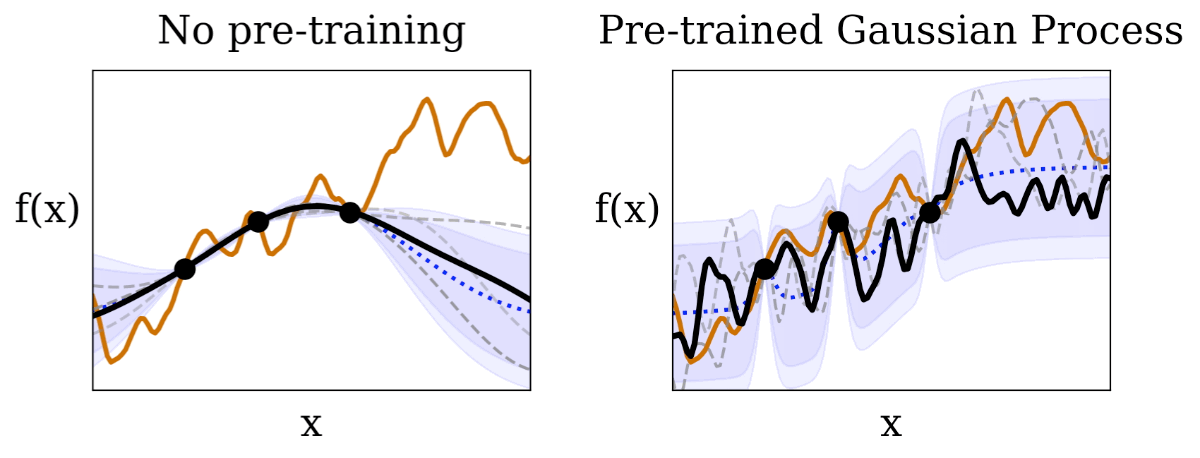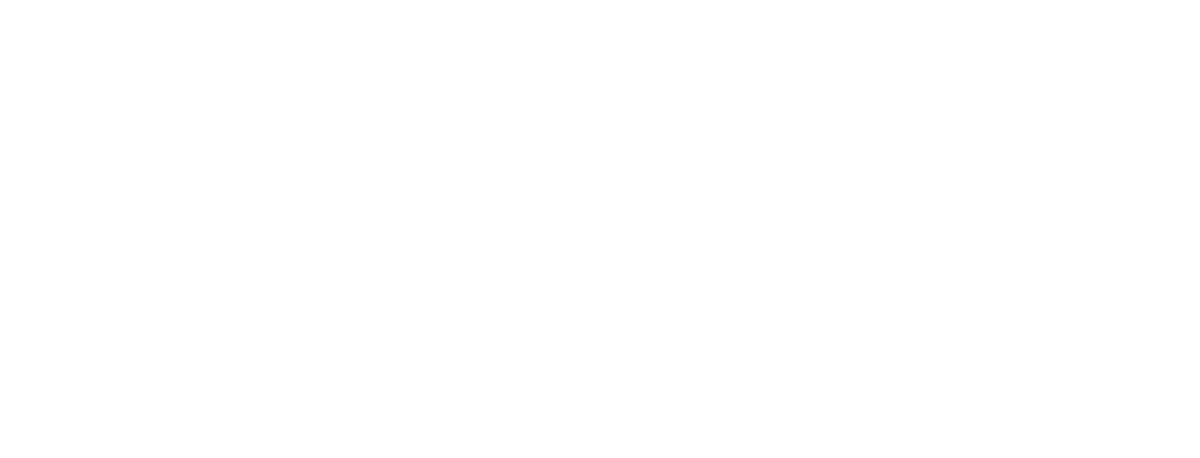| We visualize the Gaussian process (areas shaded in purple are 95% and 99% confidence intervals) conditional on observations (black dots) from an unknown test function (orange line). Compared to the traditional BayesOpt without pre-training, the predicted confidence levels in HyperBO captures the unknown test function much better, which is a critical prerequisite for Bayesian optimization. |
Empirically, to define the structure of pre-trained Gaussian processes, we choose to use very expressive mean functions modeled by neural networks, and apply well-defined kernel functions on inputs encoded to a higher dimensional space with neural networks.
To evaluate HyperBO on challenging and realistic black-box optimization problems, we created the PD1 benchmark, which contains a dataset for multi-task hyperparameter optimization for deep neural networks. PD1 was developed by training tens of thousands of configurations of near–state-of-the-art deep learning models on popular image and text datasets, as well as a protein sequence dataset. PD1 contains approximately 50,000 hyperparameter evaluations from 24 different tasks (e.g., tuning Wide ResNet on CIFAR100) with roughly 12,000 machine days of computation.
We demonstrate that when pre-training for only a few hours on a single CPU, HyperBO can significantly outperform BayesOpt with carefully hand-tuned models on unseen challenging tasks, including tuning ResNet50 on ImageNet. Even with only ~100 data points per training function, HyperBO can perform competitively against baselines.
 |
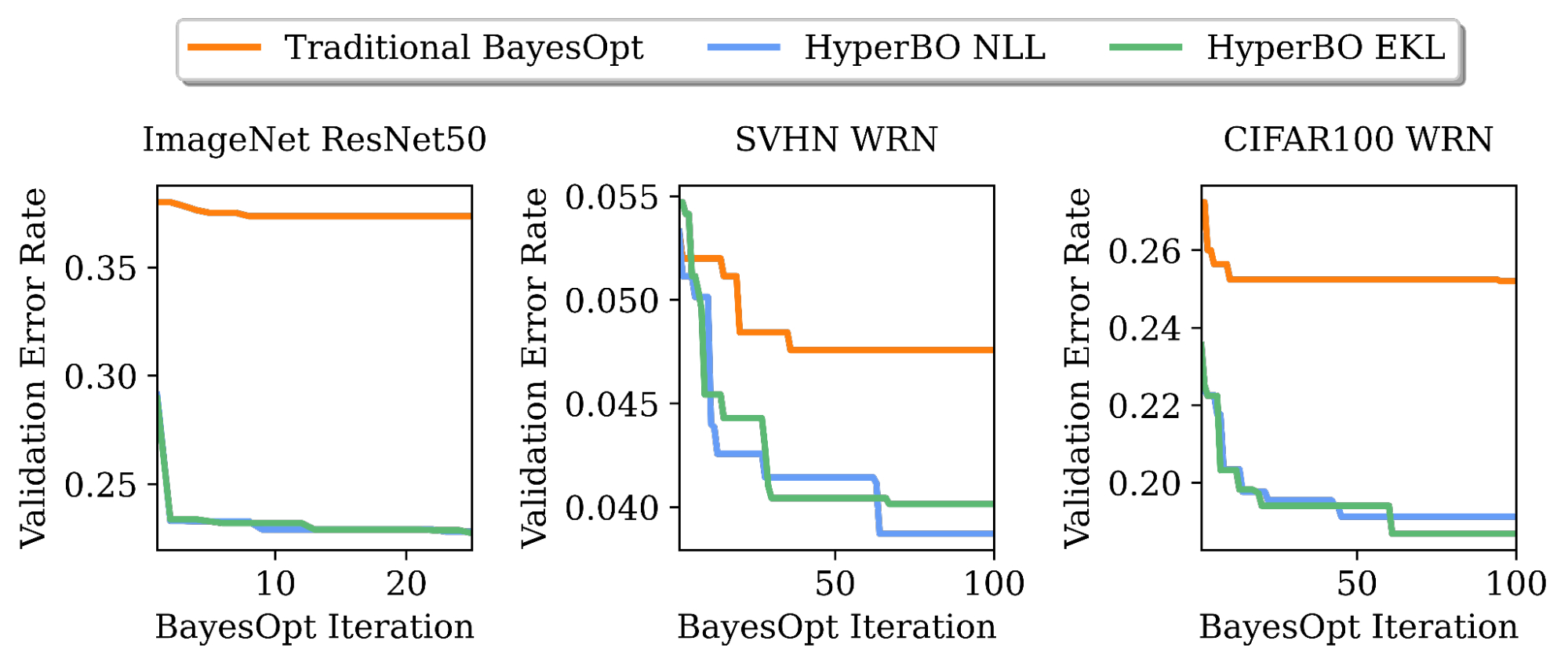| Tuning validation error rates of ResNet50 on ImageNet and Wide ResNet (WRN) on the Street View House Numbers (SVHN) dataset and CIFAR100. By pre-training on only ~20 tasks and ~100 data points per task, HyperBO can significantly outperform traditional BayesOpt (with a carefully hand-tuned Gaussian process) on previously unseen tasks. |
Conclusion and future work
HyperBO is a framework that pre-trains a Gaussian process and subsequently performs Bayesian optimization with a pre-trained model. With HyperBO, we no longer have to hand-specify the exact quantitative parameters in a Gaussian process. Instead, we only need to identify related tasks and their corresponding data for pre-training. This makes BayesOpt both more accessible and more effective. An important future direction is to enable HyperBO to generalize over heterogeneous search spaces, for which we are developing new algorithms by pre-training a hierarchical probabilistic model.
Acknowledgements
The following members of the Google Research Brain Team conducted this research: Zi Wang, George E. Dahl, Kevin Swersky, Chansoo Lee, Zachary Nado, Justin Gilmer, Jasper Snoek, and Zoubin Ghahramani. We’d like to thank Zelda Mariet and Matthias Feurer for help and consultation on transfer learning baselines. We’d also like to thank Rif A. Saurous for constructive feedback, and Rodolphe Jenatton and David Belanger for feedback on previous versions of the manuscript. In addition, we thank Sharat Chikkerur, Ben Adlam, Balaji Lakshminarayanan, Fei Sha and Eytan Bakshy for comments, and Setareh Ariafar and Alexander Terenin for conversations on animation. Finally, we thank Tom Small for designing the animation for this post.