Posted by Johan Ferret, Student Researcher, Google Research, Brain Team
An approach commonly used to train agents for a range of applications from robotics to chip design is reinforcement learning (RL). While RL excels at discovering how to solve tasks from scratch, it can struggle in training an agent to understand the reversibility of its actions, which can be crucial to ensure that agents behave in a safe manner within their environment. For instance, robots are generally costly and require maintenance, so one wants to avoid taking actions that might lead to broken components. Estimating if an action is reversible or not (or better, how easily it can be reversed) requires a working knowledge of the physics of the environment in which the agent is operating. However, in the standard RL setting, agents do not possess a model of the environment sufficient to do this.
In “There Is No Turning Back: A Self-Supervised Approach to Reversibility-Aware Reinforcement Learning”, accepted at NeurIPS 2021, we present a novel and practical way of approximating the reversibility of agent actions in the context of RL. This approach, which we call Reversibility-Aware RL, adds a separate reversibility estimation component to the RL procedure that is self-supervised (i.e., it learns from unlabeled data collected by the agents). It can be trained either online (jointly with the RL agent) or offline (from a dataset of interactions). Its role is to guide the RL policy towards reversible behavior. This approach increases the performance of RL agents on several tasks, including the challenging Sokoban puzzle game.
Reversibility-Aware RL
The reversibility component added to the RL procedure is learned from interactions, and crucially, is a model that can be trained separate from the agent itself. The model training is self-supervised and does not require that the data be labeled with the reversibility of the actions. Instead, the model learns about which types of actions tend to be reversible from the context provided by the training data alone.We call the theoretical explanation for this empirical reversibility, a measure of the probability that an event A precedes another event B, knowing that A and B both happen. Precedence is a useful proxy for true reversibility because it can be learned from a dataset of interactions, even without rewards.
Imagine, for example, an experiment where a glass is dropped from table height and when it hits the floor it shatters. In this case, the glass goes from position A (table height) to position B (floor) and regardless of the number of trials, A always precedes B, so when randomly sampling pairs of events, the probability of finding a pair in which A precedes B is 1. This would indicate an irreversible sequence. Assume, instead, a rubber ball was dropped instead of the glass. In this case, the ball would start at A, drop to B, and then (approximately) return to A. So, when sampling pairs of events, the probability of finding a pair in which A precedes B would only be 0.5 (the same as the probability that a random pair showed B preceding A), and would indicate a reversible sequence.
 |
| Reversibility estimation relies on the knowledge of the dynamics of the world. A proxy to reversibility is precedence, which establishes which of two events comes first on average,given that both are observed. |
In practice, we sample pairs of events from a collection of interactions, shuffle them, and train the neural network to reconstruct the actual chronological order of the events. The network’s performance is measured and refined by comparing its predictions against the ground truth derived from the timestamps of the actual data. Since events that are temporally distant tend to be either trivial or impossible to order, we sample events in a temporal window of fixed size. We then use the prediction probabilities of this estimator as a proxy for reversibility: if the neural network’s confidence that event A happens before event B is higher than a chosen threshold, then we deem that the transition from event A to B is irreversible.
 |
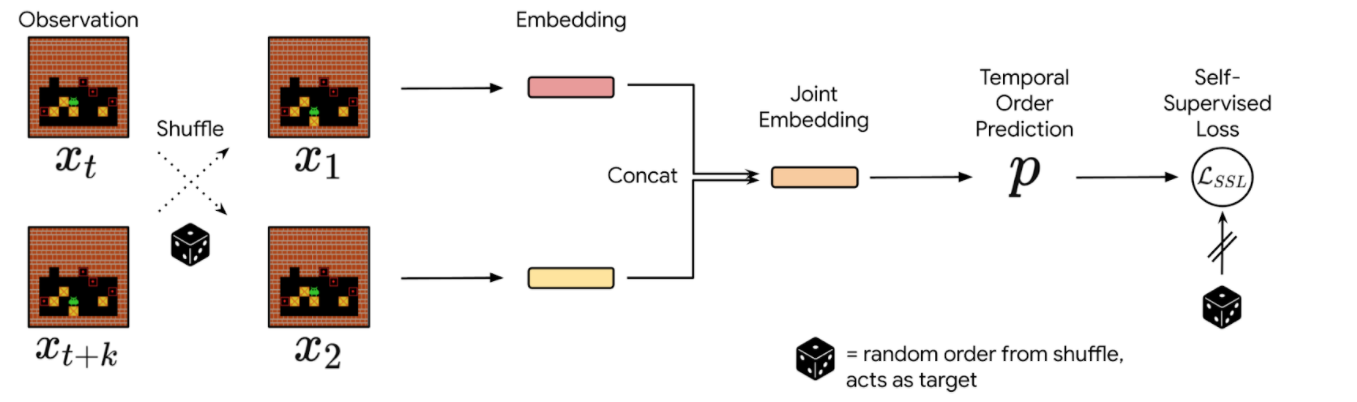| Precedence estimation consists of predicting the temporal order of randomly shuffled events. |
Integrating Reversibility into RL
We propose two concurrent ways of integrating reversibility in RL:
- Reversibility-Aware Exploration (RAE): This approach penalizes irreversible transitions, via a modified reward function. When the agent picks an action that is considered irreversible, it receives a reward corresponding to the environment’s reward minus a positive, fixed penalty, which makes such actions less likely, but does not exclude them.
- Reversibility-Aware Control (RAC): Here, all irreversible actions are filtered out, a process that serves as an intermediate layer between the policy and the environment. When the agent picks an action that is considered irreversible, the action selection process is repeated, until a reversible action is chosen.
 |
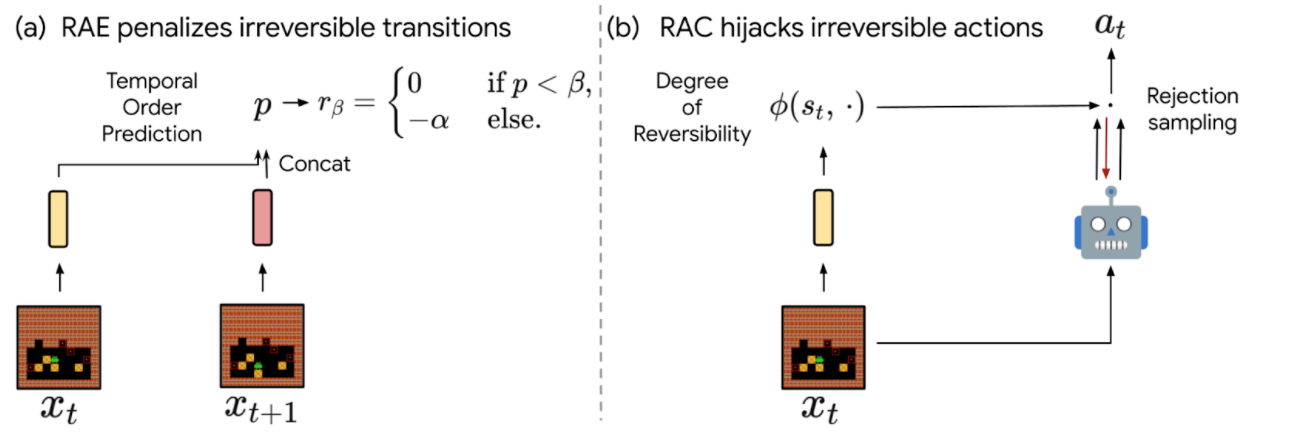| The proposed RAE (left) and RAC (right) methods for reversibility-aware RL. |
An important distinction between RAE and RAC is that RAE only encourages reversible actions, it does not prohibit them, which means that irreversible actions can still be performed when the benefits outweigh costs (as in the Sokoban example below). As a result, RAC is better suited for safe RL where irreversible side-effects induce risks that should be avoided entirely, and RAE is better suited for tasks where it is suspected that irreversible actions are to be avoided most of the time.
To illustrate the distinction between RAE and RAC, we evaluate the capabilities of both proposed methods. A few example scenarios follow:
- Avoiding (but not prohibiting) irreversible side-effects
A general rule for safe RL is to minimize irreversible interactions when possible, as a principle of caution. To test such capabilities, we introduce a synthetic environment where an agent in an open field is tasked with reaching a goal. If the agent follows the established pathway, the environment remains unchanged, but if it departs from the pathway and onto the grass, the path it takes turns to brown. While this changes the environment, no penalty is issued for such behavior.
In this scenario, a typical model-free agent, such as a Proximal Policy Optimization (PPO) agent, tends to follow the shortest path on average and spoils some of the grass, whereas a PPO+RAE agent avoids all irreversible side-effects.
Top-left: The synthetic environment in which the agent (blue) is tasked with reaching a goal (pink). A pathway is shown in grey leading from the agent to the goal, but it does not follow the most direct route between the two. Top-right: An action sequence with irreversible side-effects of an agent’s actions. When the agent departs from the path, it leaves a brown path through the field. Bottom-left: The visitation heatmap for a PPO agent. Agents tend to follow a more direct path than that shown in grey. Bottom-right: The visitation heatmap for a PPO+RAE agent. The irreversibility of going off-path encourages the agent to stay on the established grey path. - Safe interactions by prohibiting irreversibility
We also tested against the classic Cartpole task, in which the agent controls a cart in order to balance a pole standing precariously upright on top of it. We set the maximum number of interactions to 50k steps, instead of the usual 200. On this task, irreversible actions tend to cause the pole to fall, so it is better to avoid such actions at all.
We show that combining RAC with any RL agent (even a random agent) never fails, given that we select an appropriate threshold for the probability that an action is irreversible. Thus, RAC can guarantee safe, reversible interactions from the very first step in the environment.
We show how the Cartpole performance of a random policy equipped with RAC evolves with different threshold values (ꞵ). Standard model-free agents (DQN, M-DQN) typically score less than 3000, compared to 50000 (the maximum score) for an agent governed by a random+RAC policy at a threshold value of β=0.4. - Avoiding deadlocks in Sokoban
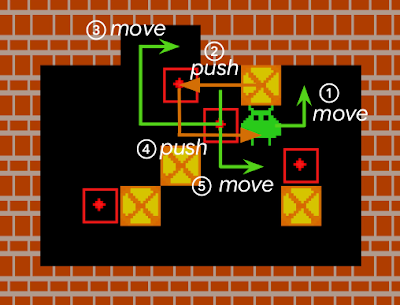
Sokoban is a puzzle game in which the player controls a warehouse keeper and has to push boxes onto target spaces, while avoiding unrecoverable situations (e.g., when a box is in a corner or, in some cases, along a wall).
An action sequence that completes a Sokoban level. Boxes (yellow squares with a red “x”) must be pushed by an agent onto targets (red outlines with a dot in the middle). Because the agent cannot pull the boxes, any box pushed against a wall can be difficult, if not impossible to get away from the wall, i.e., it becomes “deadlocked”. For a standard RL model, early iterations of the agent typically act in a near-random fashion to explore the environment, and consequently, get stuck very often. Such RL agents either fail to solve Sokoban puzzles, or are quite inefficient at it.
Agents that explore randomly quickly engage themselves in deadlocks that prevent them from completing levels (as an example here, pushing the rightmost box on the wall cannot be reversed). We compared the performance in the Sokoban environment of IMPALA, a state-of-the-art model-free RL agent, to that of an IMPALA+RAE agent. We find that the agent with the combined IMPALA+RAE policy is deadlocked less frequently, resulting in superior scores.
The scores of IMPALA and IMPALA+RAE on a set of 1000 Sokoban levels. A new level is sampled at the beginning of each episode.The best score is level dependent and close to 10. In this task, detecting irreversible actions is difficult because it is a highly imbalanced learning problem — only ~1% of actions are indeed irreversible, and many other actions are difficult to flag as reversible, because they can only be reversed through a number of additional steps by the agent.
Reversing an action is sometimes non-trivial. In the example shown here, a box has been pushed against the wall, but is still reversible. However, reversing the situation takes at least five separate movements comprising 17 distinct actions by the agent (each numbered move being the result of several actions from the agent). We estimate that approximately half of all Sokoban levels require at least one irreversible action to be completed (e.g., because at least one target destination is adjacent to a wall). Since IMPALA+RAE solves virtually all levels, it implies that RAE does not prevent the agent from taking irreversible actions when it is crucial to do so.
Conclusion
We present a method that enables RL agents to predict the reversibility of an action by learning to model the temporal order of randomly sampled trajectory events, which results in better exploration and control. Our proposed method is self-supervised, meaning that it does not necessitate any prior knowledge about the reversibility of actions, making it well suited to a variety of environments. In the future, we are interested in studying further how these ideas could be applied in larger scale and safety-critical applications.
Acknowledgements
We would like to thank our paper co-authors Nathan Grinsztajn, Philippe Preux, Olivier Pietquin and Matthieu Geist. We would also like to thank Bobak Shahriari, Théophane Weber, Damien Vincent, Alexis Jacq, Robert Dadashi, Léonard Hussenot, Nino Vieillard, Lukasz Stafiniak, Nikola Momchev, Sabela Ramos and all those who provided helpful discussion and feedback on this work.
