Sequential problem solving is a remarkable ability demonstrated by humans and other intelligent animals. For example, a behavioral ecology study has shown how a crow can plan to retrieve a stone and drop it into the box. This is not an easy task since the stone is initially placed in a cage and the crow cannot get through the bars. But the crow intelligently makes its way to the goal by sequentially picking up a stick, using the stick to reach the stone, and taking the stone to the goal location. In each step, the crow interacts with the environment in a different way which eventually serves the goal of the task. These steps need to be carefully composed together in a specific order, such that the stick will be picked up before being used for reaching the stone.

Can a robot solve sequential problems like this? Imagine if we ask the robot to push a target object to a goal position across a bridge. However, there is an obstacle object on the bridge blocking the way. The robot needs to first remove the obstacle from the bridge and then push the target object to its destination.

Solving such puzzles might seem like a no-brainer to humans, but for robots, to plan in various unseen scenarios is incredibly challenging. To achieve the goal of the task, the robot needs to choose the optimal plan among a plurality of possible solutions. Each plan is composed of a sequence of actions across the time horizon, where at each time step, the robot can take various different actions on different objects. This results in an exponentially growing space of different actions to sample from, which is further complicated by the fact that the robot also needs to predict which actions will be successful solely given the visual observations received by the camera. To find feasible solutions for multi-step manipulation tasks, we would like the robot to generate plans in a structured way and effectively rule out improbable candidates.
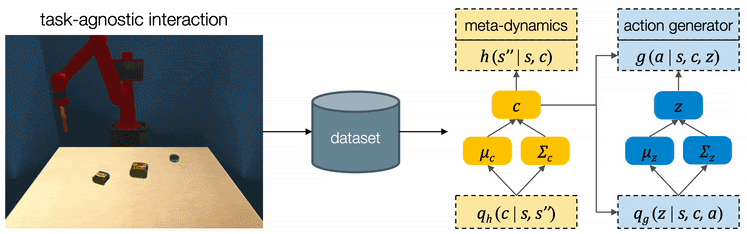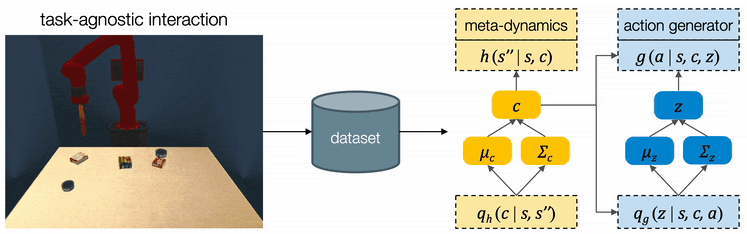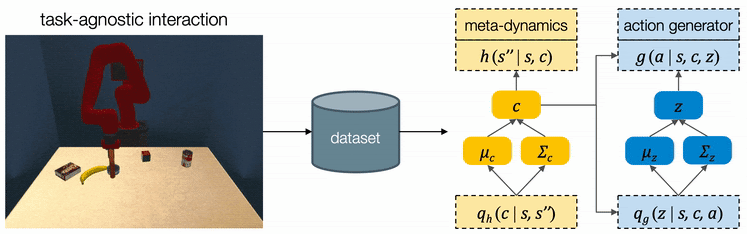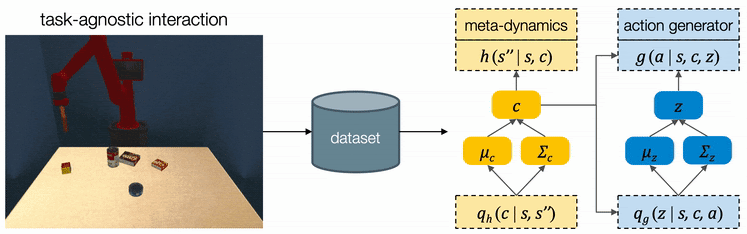
To solve these complex sequential problems, we propose CAVIN, a hierarchical planning algorithm. Our algorithm first plans for a sequence of subgoals that lead to task success and then generates actions in the context of the chosen subgoals. To prioritize promising samples, our algorithm learns to capture the distributions of reachable subgoals and feasible actions. The model can be trained with task-agonistic robot interactions and applied to different tasks.
Sampling-based Planning with Deep Generative Models
Even before we know what exactly the goal of the task is, we already know only some actions are useful for forming a promising plan. For example, if the goal is to push a target object to some target position, a push has to be applied onto an object in the first place. If a random action just waves the robot arm around or collides the arm into the table, those actions will either simply not make any progress towards the eventual goal or will violate the constraints of the environment (and hurt our robot!).
Assuming we have a dataset which contains only useful actions, we can learn to capture their distribution using deep generative models, which have been widely used for image and video synthesis. A deep generative model generates a data point given a latent code, which represents the information of the data. To sample an action, we can instead sample the latent code from its prior distribution (e.g. a Gaussian) and use the deep generative model to project it into the action. In this way, our model learns to sample with an emphasis on useful actions.
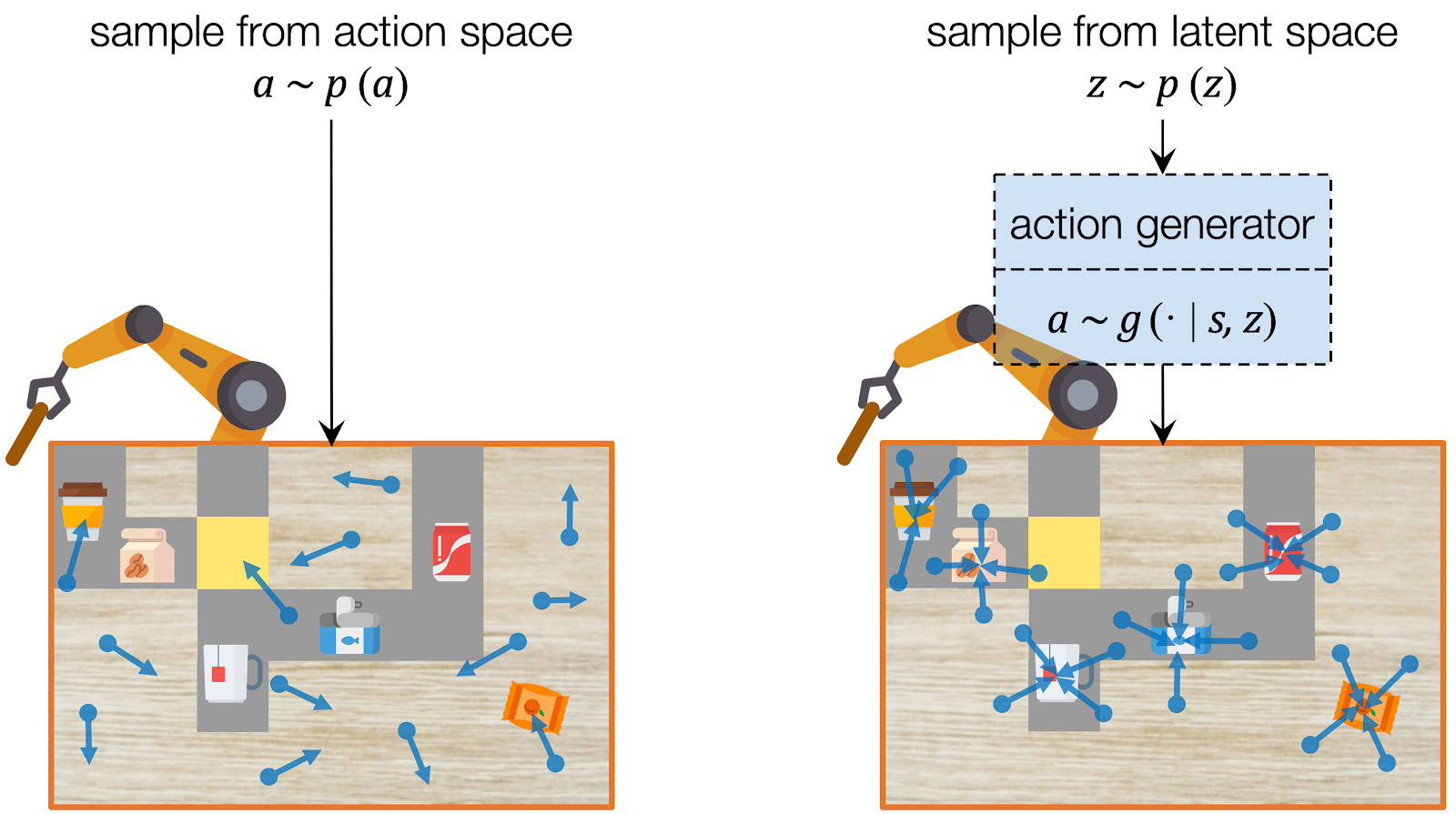
CAVIN: Hierarchical Planning in Learned Latent Spaces
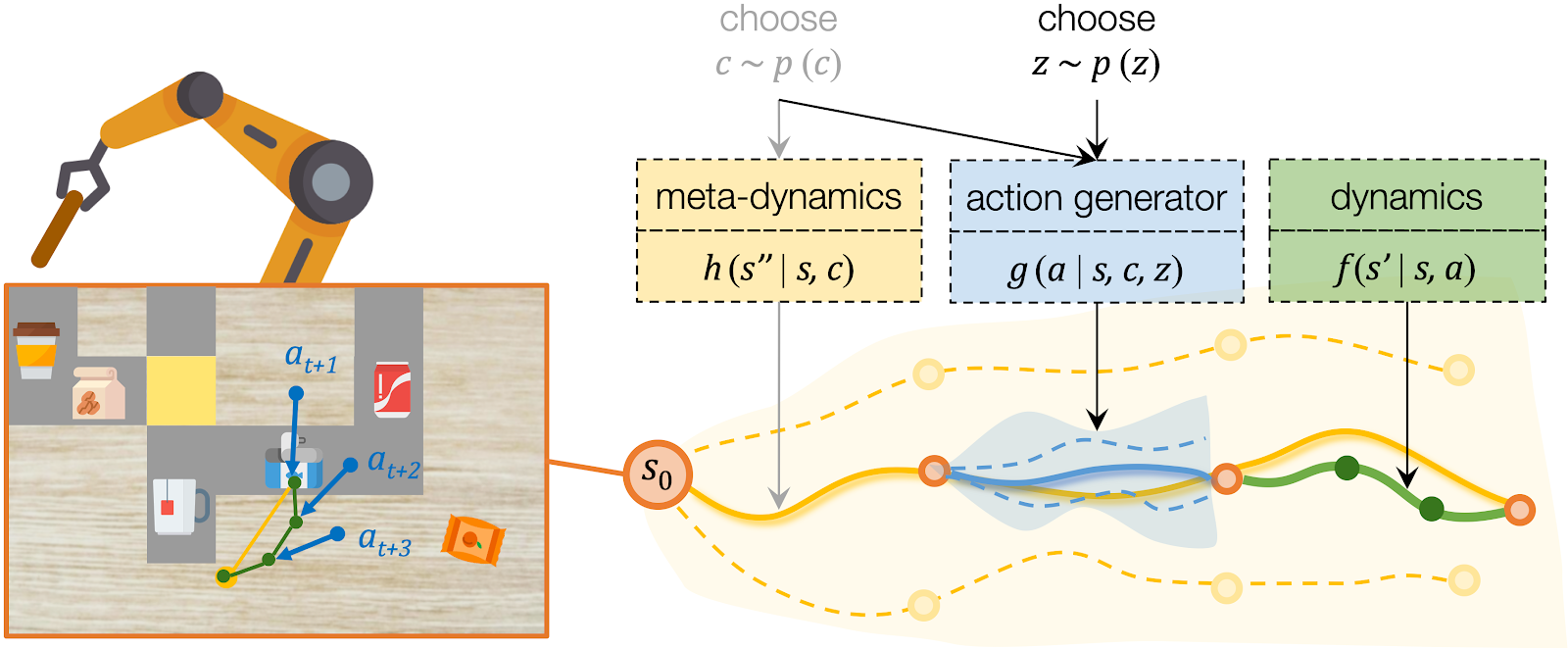
We propose CAVIN to hierarchically generate plans in learned latent spaces. To extend the aforementioned idea of learning to sample for planning with subgoals, we introduce two latent codes, effect code and motion code . Our key insight is to take advantage of the hierarchical structure of the action space, such that the generation of a plan can be factorized into a two-level process:
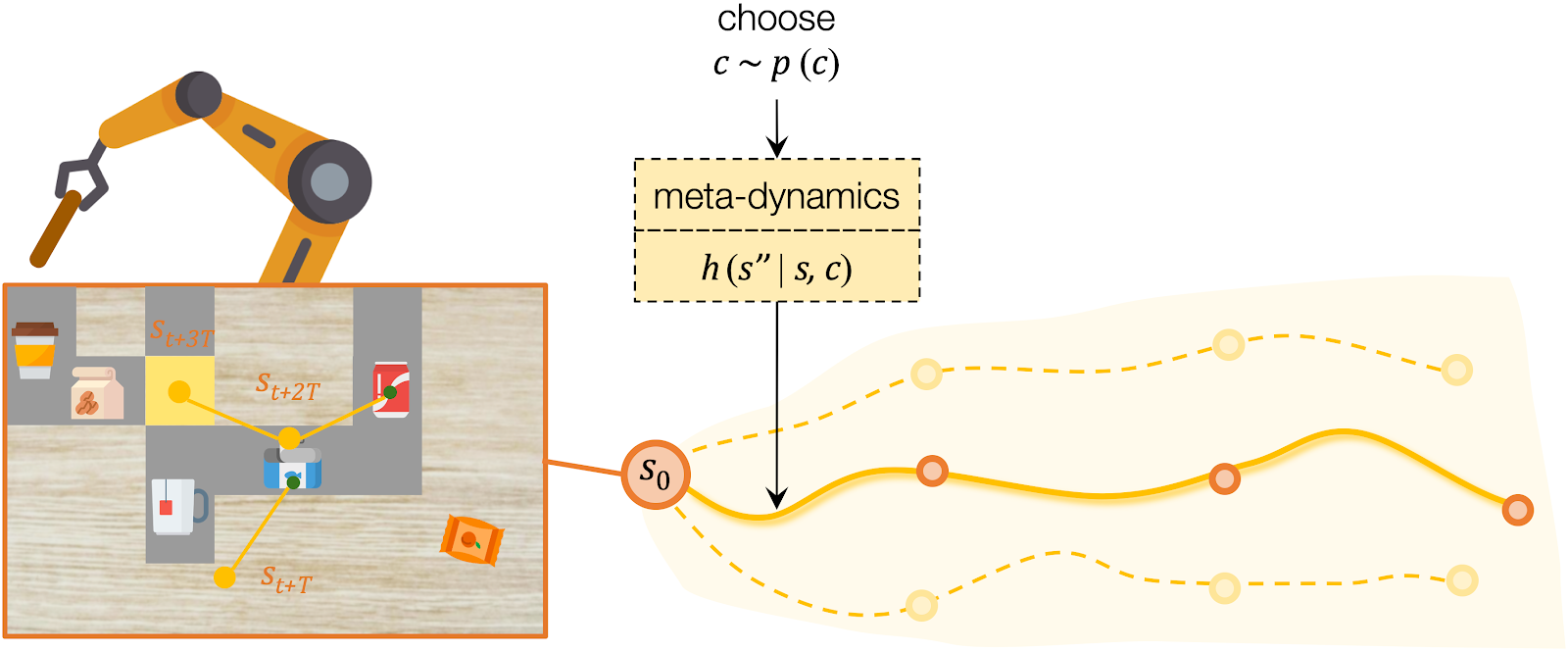
- High-level planning: Selecting the desired effects, in terms of subgoals.
- Low-level planning: Generating detailed actions that lead to the chosen subgoals.
For high-level planning, we sample and select to specify the desired subgoals every steps. Instead of predicting the environment dynamics given a sampled action, here we care about predicting what subgoal can be reached given a sampled . We call this our meta-dynamics model , which captures the distribution of reachable subgoal states
while abstracting away the detailed actions. The meta-dynamics model projects each effect code to a reachable subgoal in the future, conditioned on the current state . We sample and choose the sequence of by predicting the cumulative rewards of each sequence of subgoals.
For low-level planning, we sample and select to generate actions that will lead to the subgoals chosen by high-level planning. Action sequences is computed from the desired effect and motion by an action generator . Conditioned on the state and the chosen , the action generator projects into a plausible sequence of that will push the object towards the specified subgoal. The low-level dynamics model evaluates the generated plans by recursively predicting the resulting states . The action sequence which better reaches the subgoals will be executed by the robot.
Learning from Interactions Regardless of Tasks
We assume all tasks are performed in the same environment and the reward functions are provided to the robot as a blackbox function during test time. Therefore CAVIN can be trained in a task-agnostic fashion and later be applied to various task rewards. The data collection is conducted in a physical simulator, where we drop a variety of objects onto the table and ask the robot to randomly push around objects. We only record interesting transitions in the dataset by filtering out those which do not change the object positions or violate constraints.
We propose a cascaded variational inference algorithm to learn the meta-dynamics model and the action generator. Since the latent codes cannot be directly observed, we train the model with a lower bound objective and use two inference networks and , a to infer the latent codes from the collected transitions. To perform hierarchical planning, we need the modules to produce consistent outputs. More specifically, given a chosen , the action sequence generated from any should always yield the subgoal predicted from in the task environment. Therefore, we jointly train the modules and feed the same inferred to both the meta-dynamics model and the action generator.
Experiments
We designed three multi-step manipulation tasks: Clearing, Insertion, and Crossing. All of these tasks share the same table-top workspace and are not seen by the robot during training time. We observe that the robot comes up with diverse strategies in different task scenarios.

Open Path: When the target object is surrounded by obstacle objects, the robot opens a path for the target object (the red canned meat) towards the goal without entering the restricted area (red tiles).

Get Around: In the presence of a pile of obstacle objects between the target (the blue bag of snacks) and the goal, the robot pushes the target around.

Squeeze Through: When there is a small gap between a bunch of objects, the robot squeezes the target object (the blue tuna can) through the gap.

Move Away Obstacles: When pushing the target object (the red jello box) across the bridge (grey tiles), the robot clears obstacle objects one by one along the way.

Push Target Through Obstacles: When the robot cannot directly reach the target object (tuna can), it squeezes the target object by pushing obstacle objects.

Clean up a workspace: The robot moves objects out of a designated workspace (blue tiles).

Summary
We proposed CAVIN, a hierarchical planning algorithm in learned latent spaces. Using deep generative models, CAVIN prioritizes useful actions in sampling-based planning. The planning process is factored into two levels by subgoals to effectively generate plans. A cascaded variational inference framework is used to learn CAVIN from task-agnostic interactions. Our method enables the robot to effectively perform multi-step manipulation tasks in cluttered tabletop environments given high-dimensional visual inputs.
We expect to apply CAVIN in more challenging multi-step manipulation tasks in the future. While the core algorithm is not limited to the planar pushing actions demonstrated in this work, how to effectively solve sequential problems which require diverse robot skills such as grasping, sweeping, hammering, etc. still remains an open question. While in our tasks we assume all objects are placed on the table without occlusions, the robot will need to explicitly deal with partial observations in more complex environments.
For more information please refer to the project website. We’ve also released our codebase and the robotic task environments in simulation and the real world.
This blog post was based on the following paper: Dynamics Learning with Cascaded Variational Inference for Multi-Step Manipulation. K. Fang, Y. Zhu, A. Garg, S.Savarese, L. Fei-Fei. In Conference on Robot Learning, 2019. (pdf)
